
科目: 来源:江西省南昌市2018届九年级(上)期中数学试卷 题型:解答题
在实数范围内定义一种新运算“#”,其规则时:a#b=a2﹣b2.
(1)求4#3与(﹣1)#(﹣2)的值;
(2)求(x+2)#5=0中的x值.
(1)7,-3;(2)x1=3或x2=﹣7. 【解析】试题分析:根据a#b=a2﹣b2,可得答案. 试题解析:【解析】 (1)4#3=42﹣32=7,(﹣1)#(﹣2)=(﹣1)2﹣(﹣2)2=﹣3; (2)由题意得:(x+2)2﹣52=0,解得x+2=±5,∴ x1=3,x2=﹣7.查看答案和解析>>
科目: 来源:江西省南昌市2018届九年级(上)期中数学试卷 题型:解答题
已知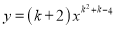 是二次函数,且函数图象有最高点.
是二次函数,且函数图象有最高点.
(1)求k的值;
(2)求顶点坐标和对称轴,并说明当x为何值时,y随x的增大而减少.
(1)k=﹣3;(2)当k=﹣3时,y=﹣x2顶点坐标(0,0),对称轴为y轴,当x>0时,y随x的增大而减少. 【解析】试题分析:(1)根据二次函数的定义得出k2+k﹣4=2,再利用函数图象有最高点,得出k+2<0,即可得出k的值; (2)利用(1)中k的值得出二次函数的解析式,利用形如y=ax2(a≠0)的二次函数顶点坐标为(0,0),对称轴是y轴即可得出答案. 试题解析:【...查看答案和解析>>
科目: 来源:江西省南昌市2018届九年级(上)期中数学试卷 题型:解答题
已知关于x的一元二次方程x2-2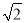 x+m=0有两个不相等的实数根.
x+m=0有两个不相等的实数根.
(1)求实数m的最大整数值;
(2)在(1)的条件下,方程的实数根是x1,x2,求代数式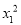 +
+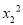 -
-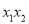 的值.
的值.
查看答案和解析>>
科目: 来源:江西省南昌市2018届九年级(上)期中数学试卷 题型:解答题
如图,均为7×6的正方形网格,点A、B、C均在格点(小正方形的顶点)上,在图中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其满足下列条件(三个图形互不相同):
(1)在图①中所画的四边形中,∠D为钝角,且四边形是轴对称图形.
(2)在图②中所画的四边形中,∠D为锐角,且四边形是中心对称图形.
(3)在图③所画的四边形中,∠D为直角,且四边形面积为5平方单位.

查看答案和解析>>
科目: 来源:江西省南昌市2018届九年级(上)期中数学试卷 题型:解答题
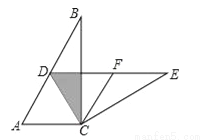
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按照顺时针方向旋转m度后得到△DEC,点D刚好落在AB边上.
(1)求m的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
科目: 来源:江西省南昌市2018届九年级(上)期中数学试卷 题型:解答题
某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
(1)y=﹣2x+80;(2)每本纪念册的销售单价是25元;(3)该纪念册销售单价定为28元时,才能使文具店销售该纪念册所获利润最大,最大利润是192元. 【解析】试题分析:(1)待定系数法列方程组求一次函数解析式. (2)列一元二次方程求解. (3)总利润=单件利润销售量:w=(x-20)(-2x+80),得到二次函数,先配方,在定义域上求最值. 试题解析: (1)...查看答案和解析>>
科目: 来源:江西省南昌市2018届九年级(上)期中数学试卷 题型:解答题
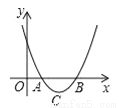
如图,已知抛物线y=x2﹣4x+3与x轴交于A,B两点,其顶点为C.
(1)对于任意实数m,点M(m,﹣2)是否在该抛物线上?请说明理由;
(2)求证:△ABC是等腰直角三角形;
(3)若点D在x轴上,则在抛物线上是否存在点P,使得PD∥BC,且PD=BC?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:江西省南昌市2018届九年级(上)期中数学试卷 题型:解答题
(1)如图(1),在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
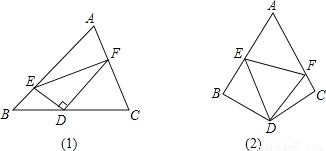
①求证:BE+CF>EF.
②若∠A=90°,探索线段BE、CF、EF之间的数量关系,并加以证明;
(2)如图(2),在四边形ABCD中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
(1)①见解析;②BE2+CF2=EF2.证明见解析;(2)EF= EB+CF,证明见解析. 【解析】 试题分析:(1)①如图(1)延长ED到G,使DG=ED,连接CG,FG,根据条件证明△DCG≌△DBE,得DG=DE,CG=BE,易证FD垂直平分线段EG,则FG=FE,把问题转化到△CFG中,运用三边关系比较大小; ②结论:BE2+CF2=EF2.若∠A=90°,则∠B+∠C...查看答案和解析>>
科目: 来源:浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型:单选题
下列四个图形中,是轴对称图形的是( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源:浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型:单选题
若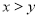 ,则下列式子中错误的是( ).
,则下列式子中错误的是( ).
A. 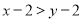 B.
B. 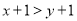 C.
C. 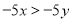 D.
D. 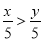
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com