等腰三角形的周长为16，其中一条边的长是6，求另两条边的长．

另两边长分别是6、4或者5、5． 【解析】试题分析：首先根据题意分情况进行讨论，（1）若8cm为腰，然后根据等腰三角形的性质和三角形周长公式计算另两条边的长度即可，（2）若8cm为底边，则等腰三角形的腰长=（20﹣8）÷2=6． 试题解析：（1）如果6为腰， 底边=16﹣6×2=4， （2）如果6为底， 腰长（16﹣6）÷2=5， 答：另两边长分别是6、4或者5...

下列是胡老师带领学生，探究SSA是否能判定两个三角形全等的过程，填空．

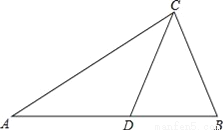
如图：已知CD=CB，

在△ABC和△ADC中，

AC=_____，（公共边）

CB=CD，（已知）

∠A=∠A，（_______）

则△ABC和△ADC满足两边及一边的对角分别相等，即满足_____，

很显然：△ABC_____△ADC，（填“全等于”或“不全等于”）

下结论：SSA_____（填“能”或“不能”）判定两个三角形全等．

AC 公共角 SSA 不全等于 不能 【解析】试题分析：根据图形，即可作出解答． 试题解析：下列是胡老师带领学生，探究SSA是否能判定两个三角形全等的过程，填空． 如图：已知 在和中， ，（公共边） ，（已知） （ 公共角） 则和满足两边及一边的对角分别相等，即满足SSA， 很显然： 不全等于，（填“全等于”或“不全等于”） 下结论：SS...

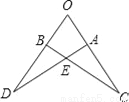
如图，若△OAD≌△OBC，且∠O=65°，∠C=20°，求∠OAD的度数．

95° 【解析】试题分析：根据三角形内角和定理求出根据全等三角形的对应角相等解答． 试题解析： ≌

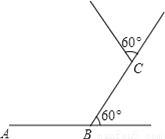
如图，小东在足球场的中间位置，从A点出发，每走6m向左转60°，已知AB=BC=6m．

（1）小东是否能走回A点，若能回到A点，则需走几m，走过的路径是一个什么图形？为什么？（路径A到B到C到…）

（2）求出这个图形的内角和．

（1）走过的路径是一个边长为6的正六边形；（2）720°． 【解析】试题分析：1）利用外角和为360°计算出多边形的边数即可； （2）利用内角和公式直接计算即可． 试题解析：（1）从A点出发，每走6m向左转60°， 走过的路径是一个边长为6的正六边形； （2）正六边形的内角和为：（6﹣2）×180°=720°．

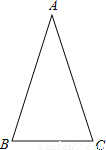
如图，在△ABC中，AB=AC，∠ABC=72°．

（1）用直尺和圆规作∠ABC的平分线BD交AC于点D（保留作图痕迹，不要求写作法）；

（2）在（1）中作出∠ABC的平分线BD后，求∠BDC的度数．

（1）作图见解析；（2）72°． 【解析】试题分析：（1）根据角平分线的作法利用直尺和圆规作出∠ABC的平分线即可； （2）先根据等腰三角形的性质及三角形内角和定理求出∠A的度数，再由角平分线的定义得出∠ABD的度数，再根据三角形外角的性质得出∠BDC的度数即可． 试题解析：（1）①一点B为圆心，以任意长长为半径画弧，分别交AB、BC于点E、F； ②分别以点E、F为圆心，以...

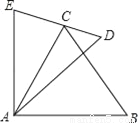
已知，如图AE=AC，AD=AB，∠EAC=∠DAB．

求证：（1）△EAD≌△CAB；

（2）∠DCB=∠BAD．

见解析 【解析】试题分析：（1）易证 即可证明≌ （2）根据（1）中结论可得 根据 即可求得 即可解题． 试题解析：证明：（1） 即 在和中， ≌（SAS）； （2）≌

如图所示，E、F分别为线段AC上的两个点，且DE⊥AC于点E，BF⊥AC于点F，若AB=CD，AE=CF，BD交AC于点M．

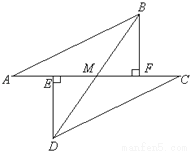
（1）试猜想DE与BF的关系，并证明你的结论；

（2）求证：MB=MD．

（1）BF=DE；（2）证明见解析 【解析】 试题分析：（1）根据DE⊥AC，BF⊥AC可以证明DE∥BF；再求证Rt△ABF≌Rt△CDE可得BF=DE，即可解题； （2）根据（1）中结论可证△DEM≌△BFM，即可解题． 【解析】 （1）DE=BF，且DE∥BF， 证明：∵DE⊥AC，BF⊥AC， ∴∠DEC=∠BFA=90°． ∴DE∥BF， ...

如图（1），Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D。AF平分∠CAB，交CD于点E，交CB于点F。

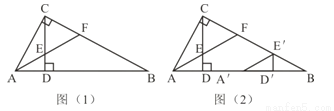
（1）求证：CE=CF。

（2）将图（1）中的△ADE沿AB向右平移到△A′D′E′的位置，使点E′落在BC边上，其它条件不变，如图(2)所示。试猜想：BE′与CF有怎样的数量关系？请证明你的结论。

（1）见解析证明；（2）=CF．理由见解析证明． 【解析】 试题分析：（1）根据角平分线的定义可得∠CAF=∠EAD，再根据等角的余角相等求出∠CFA=∠AED ，然后根据对顶角相等可得∠AED=∠CEF，从而得到∠CFA=∠AED，再根据等角对等边证明即可；（2）过点E作EG⊥AC于点G，根据角平分线的性质得到ED=EG，根据平移的性质可得=DE，然后求出∠ACD=∠B，再利用“角角...

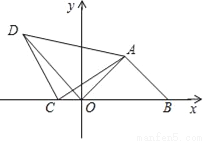
如图，在平面直角坐标系中，△AOB为等腰直角三角形，AB=OA，B（8，0），△ACD为x轴上方的等腰直角三角形，∠ACD=90°，连OD．

（1）A点的坐标为_____；

（2）作CH⊥x轴交AO的延长线于点H，

①求证：△DCO≌△ACH；

②求∠AOD的度数；

（3）若点C在x轴负半轴上运动时，其它条件不变，∠AOD的度数会发生变化吗？请说明你的理由．

（4，4） 【解析】试题分析：（1）作 易证，即可求得A点坐标； （2）①作出图形，易证 即可证明≌ 即可解题； ②根据①中结论可得即可求得 即可解题； （3）由（2）中②可得 大小和C点位置无关． 试题解析：（1）作 为等腰直角三角形， 点A坐标（4，4）， 故答案为（4，4）； （2）∵如图，作轴交AO的延长线于点H， ∴点C只能在轴...

下列方程中是一元一次方程的是（　　）

A. x+3=y+2 B. x+3=3﹣x C. 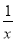=1 D. x2﹣1=0

B 【解析】只含有一个未知数（元），并且未知数的最高次数是1（次）的方程叫做一元一次方程．据此可得出： A、含有两个未知数，是二元一次方程； B、符合一元一次方程的定义； C、分母中含有未知数，是分式方程； D、未知数的最高次数实2次，为一元二次方程． 故选：B.