
科目: 来源:浙江省杭州市2018届九年级上学期期中数学试卷 题型:填空题
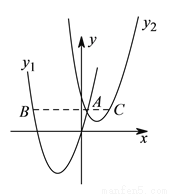
如图,将二次函数 的图像向上平移
的图像向上平移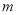 个单位得到二次函数
个单位得到二次函数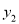 的图像,且与二次函数
的图像,且与二次函数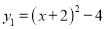 的图像相交于
的图像相交于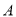 ,过
,过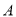 作
作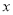 轴的平行线分别交
轴的平行线分别交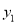 ,
, 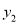 于点
于点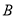 ,
, 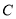 ,当
,当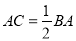 时,
时, 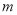 的值是__________.
的值是__________.
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中数学试卷 题型:解答题
如图:电路图上有四个开关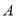 、
、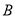 、
、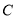 、
、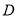 和一个小灯泡,闭合开关
和一个小灯泡,闭合开关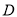 或同时闭合开关
或同时闭合开关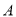 ,
, 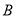 ,
, 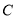 都可使小灯泡发光.
都可使小灯泡发光.
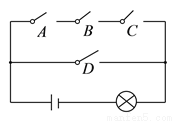
(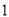 )任意闭合其中一个开关,则小灯泡发光的概率等于__________.
)任意闭合其中一个开关,则小灯泡发光的概率等于__________.
(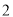 )任意闭合其中两个开关,请画树状图或列表的方法求出小灯泡发光的概率.
)任意闭合其中两个开关,请画树状图或列表的方法求出小灯泡发光的概率.
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中数学试卷 题型:解答题
已知:如图,在⊙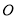 中,
中, 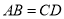 ,
, 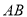 与
与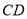 相交于点
相交于点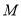 ,求证:
,求证: 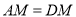 .
.

查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中数学试卷 题型:解答题
若函数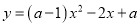 的图象与坐标轴有两个交点,求
的图象与坐标轴有两个交点,求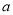 的值.
的值.
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中数学试卷 题型:解答题
已知:如图, 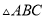 内接于⊙
内接于⊙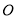 ,
, 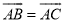 ,
, 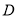 是
是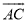 上一点(不与点
上一点(不与点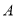 ,
, 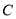 重合),延长
重合),延长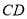 至点
至点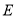 .
.

(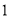 )求证:
)求证: 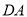 平分
平分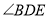 .
.
( )若
)若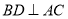 于点
于点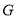 ,
, 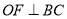 于点
于点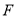 ,求证:
,求证: 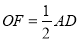 .
.
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中数学试卷 题型:解答题
已知二次函数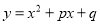 图象的顶点
图象的顶点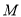 为直线
为直线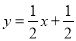 与
与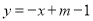 的交点.
的交点.
(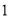 )用含
)用含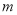 的代数式来表示顶点
的代数式来表示顶点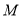 的坐标.
的坐标.
(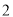 )当
)当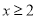 时,二次函数
时,二次函数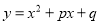 与
与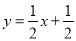 的值均随
的值均随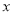 的增大而增大,求
的增大而增大,求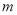 的取值范围.
的取值范围.
(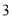 )若
)若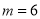 ,当
,当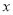 取值为
取值为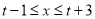 时,二次函数
时,二次函数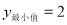 ,求
,求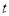 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中数学试卷 题型:解答题
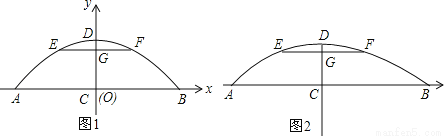
一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米.
(1)如图1,若把桥看做是抛物线的一部分,建立如图坐标系.
①求抛物线的解析式;
②要使高为3米的船通过,则其宽度须不超过多少米?
(2)如图2,若把桥看做是圆的一部分.
①求圆的半径;
②要使高为3米的船通过,则其宽度须不超过多少米?
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中数学试卷 题型:解答题
已知,抛物线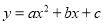 ( a≠0)经过原点,顶点为A(h,k)(h≠0).
( a≠0)经过原点,顶点为A(h,k)(h≠0).
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线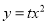 (t≠0)也经过A点,求a与t之间的关系式;
(t≠0)也经过A点,求a与t之间的关系式;
(3)当点A在抛物线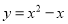 上,且-2≤h<1时,求a的取值范围.
上,且-2≤h<1时,求a的取值范围.
查看答案和解析>>
科目: 来源:浙江省杭州市西湖区绿城育华2017-2018学年八年级上学期期中数学试卷 题型:单选题
给出下面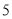 个式子:①
个式子:①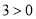 ;②
;②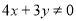 ;③
;③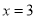 ;④
;④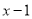 ;⑤
;⑤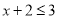 ,其中不等式有( ).
,其中不等式有( ).
A. 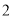 个 B.
个 B. 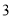 个 C.
个 C. 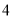 个 D.
个 D. 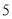 个
个
查看答案和解析>>
科目: 来源:浙江省杭州市西湖区绿城育华2017-2018学年八年级上学期期中数学试卷 题型:单选题
下列各组数中,不可能成为一个三角形三边长的是( ).
A. 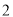 ,
, 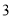 ,
, 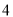 B.
B. 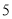 ,
, 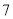 ,
, 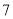 C.
C. 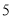 ,
, 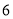 ,
, 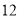 D.
D. 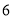 ,
, 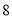 ,
, 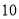
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com