
科目: 来源:贵州省遵义市桐梓县2017届九年级上学期期末考试数学试卷 题型:填空题
已知二次函数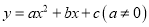 的图像,有下列4个结论:①
的图像,有下列4个结论:①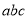 >0;②
>0;②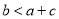 ;③
;③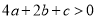 ; ④
; ④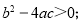 其中正确的结论有_______.(填序号)
其中正确的结论有_______.(填序号)
查看答案和解析>>
科目: 来源:贵州省遵义市桐梓县2017届九年级上学期期末考试数学试卷 题型:解答题
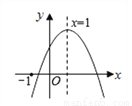
△ABC三个顶点A,B,C在平面直角坐标系中位置如图所示.将△ABC绕C点顺时针旋转90°,画出旋转后的△A2B2C2,并写出A2,B2的坐标.
查看答案和解析>>
科目: 来源:贵州省遵义市桐梓县2017届九年级上学期期末考试数学试卷 题型:解答题
(1)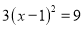 (2)
(2) 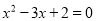
查看答案和解析>>
科目: 来源:贵州省遵义市桐梓县2017届九年级上学期期末考试数学试卷 题型:解答题
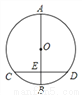
如图所示,在⊙O中直径AB垂直于弦CD,垂足为E,若BE=2 ,CD=6
,CD=6 .求⊙O的半径.
.求⊙O的半径.
查看答案和解析>>
科目: 来源:贵州省遵义市桐梓县2017届九年级上学期期末考试数学试卷 题型:解答题
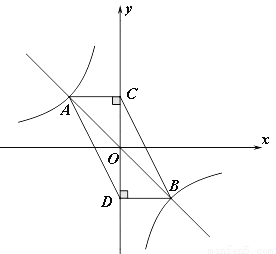
如图,函数y=?x的图象与函数y=?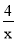 的图象相交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,D,则四边形ACBD的面积为 .
的图象相交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,D,则四边形ACBD的面积为 .
查看答案和解析>>
科目: 来源:贵州省遵义市桐梓县2017届九年级上学期期末考试数学试卷 题型:解答题
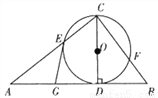
如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA, CB于点E,F,点G是AD的中点.求证:GE是⊙O的切线.
查看答案和解析>>
科目: 来源:贵州省遵义市桐梓县2017届九年级上学期期末考试数学试卷 题型:解答题
一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为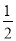 .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,
求两次摸 出都是红球的概率;
(1)1;(2) 【解析】试题分析: (1)设口袋中黄球的个数为x个,根据从中任意摸出一个球是红球的概率为和概率公式列出方程,解方程即可求得答案;(2)根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出都是红球的情况,再利用概率公式即可求得答案; 试题解析: 【解析】 (1)设口袋中黄球的个数为个, 根据题意得: 解得: =1 经检验: =1是原分...查看答案和解析>>
科目: 来源:贵州省遵义市桐梓县2017届九年级上学期期末考试数学试卷 题型:解答题
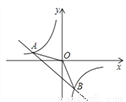
一次函数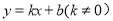 与反比列函数
与反比列函数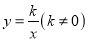 的图像交于A(-2,1),B(1,
的图像交于A(-2,1),B(1, )两点,求△ABO的面积.
)两点,求△ABO的面积.
查看答案和解析>>
科目: 来源:贵州省遵义市桐梓县2017届九年级上学期期末考试数学试卷 题型:解答题
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元。为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。求:
⑴若商场平均每天要盈利1200元,每件衬衫应降价多少元?
⑵每件衬衫降价多少元,商场平均每天盈利最多,最多盈利是多少元?
(1)20.(2)15,1250. 【解析】试题分析:(1)首先设每件寸衫应降价x元,然后根据总利润=单件利润×数量列出方程进行求解;(2)、根据二次函数的顶点式得出最大值. 试题解析:(1)设每件衬衫应降价x元。 根据题意,得 (40-x)(20+2x)=1200 整理,得x2-30x+200=0 解之得 x1=10,x2=20。 因题意要尽快减少库存,所以x取20。 ...查看答案和解析>>
科目: 来源:贵州省遵义市桐梓县2017届九年级上学期期末考试数学试卷 题型:解答题
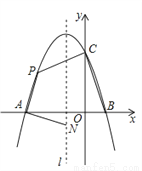
如图,抛物线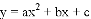
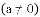 与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴
与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴
(1)求抛物线的解析式并写出其顶点坐标;
(2)当点P的纵坐标为2时,求点P的横坐标;
(3)当点P在运动过程中,求四边形PABC面积最大时的值及此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com