
科目: 来源:九年级数学第一学期1.3.2正方形的判定 同步练习 题型:单选题
在四边形ABCD中,AC、BD相交于O,能判定这个四边形是正方形的是( )
A. AO=BO=CO=DO,AC⊥BD B. AB∥CD,AC=BD
C. AO=BO,∠A=∠C D. AO=CO,BO=DO,AB=BC
A 【解析】试题分析:根据正方形的判定定理一次分析各项即可判断. A. AO=BO=CO=DO,AC⊥BD,能判定,本选项正确; B. AB∥CD,AC=BD,C. AD∥BC,∠A=∠C,D. AO=CO,BO=CO,AB=BC,均不能判定.查看答案和解析>>
科目: 来源:九年级数学第一学期1.3.2正方形的判定 同步练习 题型:填空题
已知直角三角形ABC,∠ABC=90°,AB=3,BC=5,以AC为边向外作正方形ACEF,则这个正方形的中心O到点B的距离为______.
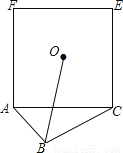
查看答案和解析>>
科目: 来源:九年级数学第一学期1.3.2正方形的判定 同步练习 题型:填空题
如图,已知正方形ABCD的对角线交于点O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF等于________.
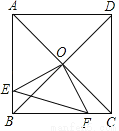
查看答案和解析>>
科目: 来源:九年级数学第一学期1.3.2正方形的判定 同步练习 题型:填空题
如图,正方形ABCD的边长为15,AG=CH=12,BG=DH=9,连接GH,则线段GH的长为______.
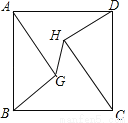
查看答案和解析>>
科目: 来源:九年级数学第一学期1.3.2正方形的判定 同步练习 题型:解答题
平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.
(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;
(2)当四边形ABCD是 形时,四边形OBEC是正方形.
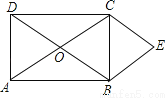
查看答案和解析>>
科目: 来源:九年级数学第一学期1.3.2正方形的判定 同步练习 题型:解答题
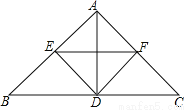
如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.
(1)求证:△BDE≌△CDF;
(2)若BC=2AD,求证:四边形AEDF是正方形.
查看答案和解析>>
科目: 来源:九年级数学第一学期1.3.2正方形的判定 同步练习 题型:解答题
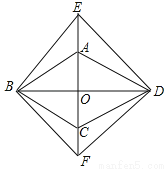
如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
(1)求证:△BAE≌△BCF;
(2)若∠ABC=40°,则当∠EBA= 时,四边形BFDE是正方形.
查看答案和解析>>
科目: 来源:九年级数学第一学期1.3.2正方形的判定 同步练习 题型:解答题
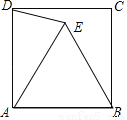
如图所示,点E为正方形ABCD内部的一点,且△ABE为等边三角形,试求∠ADE的度数.
查看答案和解析>>
科目: 来源:九年级数学第一学期1.3.2正方形的判定 同步练习 题型:解答题
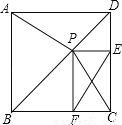
如图,P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足.
(1)求证:△APD≌△CPD;
(2)若CF=3,CE=4,求AP的长.
查看答案和解析>>
科目: 来源:九年级数学第一学期1.3.2正方形的判定 同步练习 题型:解答题
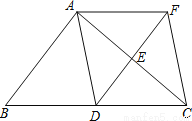
如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com