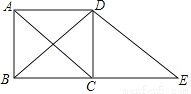
如图，在矩形ABCD中，连接对角线AC，BD，延长BC至点E，使BC=CE，连接DE．

求证：DE=AC．

证明见解析 【解析】试题分析： 证明CD是线段BE的垂直平分线，得到DB=DE，又因为DB=AC，则得证. 试题解析： ∵四边形ABCD是矩形，∴AC=BD，∠BCD=90°， ∵BC=CE，∴DC是BE的中垂线，∴BD=DE， ∴DE=AC．

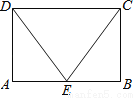
如图，在矩形ABCD中．点E在边AB上，∠CDE=∠DCE．

求证：AE=BE．

证明见解析 【解析】试题分析： 因为∠CDE=∠DCE，所以ED=EC，则可用HL证明Rt△DAE≌Rt△CBE，从而得AE=BE. 试题解析： ∵四边形ABCD是矩形， ∴∠A=∠B=90°，AD=BC， ∵∠CDE=∠DCE， ∴DE=CE， 在Rt△DAE和Rt△CBE中，， ∴Rt△DAE≌Rt△CBE（HL）， ∴AE=BE． ...

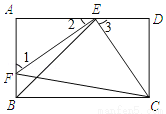
如图，E，F分别是矩形ABCD的边AD，AB上的点，若EF=EC，且EF⊥EC．

（1）求证：△AEF≌△DCE；

（2）若CD=1，求BE的长．

（1）证明见解析（2） 【解析】试题分析：（1）根据矩形的性质和已知条件可证明△AEF≌△DCE； （2）由（1）可知AE=DC，在Rt△ABE中由勾股定理可求得BE的长 试题解析：（1）证明：在矩形ABCD中，∠A=∠D=90°， ∴∠1+∠2=90°， ∵EF⊥EC， ∴∠FEC=90°， ∴∠2+∠3=90°， ∴∠1=∠3， 在△AEF...

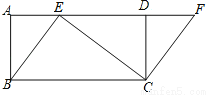
如图，四边形ABCD是矩形，点E在AD边上，点F在AD的延长线上，且BE=CF．

（1）求证：四边形EBCF是平行四边形．

（2）若∠BEC=90°，∠ABE=30°，AB=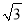，求ED的长．

（1）证明见解析（2）3 【解析】试题分析： （1）由AB=CD，BE=CF，可证Rt△BAE≌Rt△CDF，从而证得BE∥CF，即可得证； （2）由题意可知∠2=30°，∠1=∠3=60°，在直角△ABE中求出AE，BE，在直角△BEC中求出BC的长，即可求出ED的长. 试题解析： （1）证明： ∵四边形ABCD是矩形，∴∠A=∠CDF=∠ABC=90°，AB...

如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（　　）

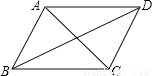
A. 当AB=BC时，四边形ABCD是菱形

B. 当AC⊥BD时，四边形ABCD是菱形

C. 当∠ABC=90°时，四边形ABCD是矩形

D. 当AC=BD时，四边形ABCD是正方形

D 【解析】A.因为有一组邻边相等的平行四边形叫做菱形，所以A正确； B.因为对角线相等的平行四边形是菱形，所以B正确； C.因为有一个角是直角的平行四边形是矩形，所以C正确； D.对角线相等的平行四边形是矩形，不一定是正方形，所以D错误. 故选D.

下列说法中错误的是（　　）

A. 平行四边形的对角线互相平分

B. 两组对边分别相等的四边形是平行四边形

C. 矩形的对角线相等

D. 有一组邻边相等且有一个角是直角的四边形是正方形

D 【解析】根据平行四边形的性质可知，A，B正确；根据矩形的性质，C正确；有一组邻边相等且有一个角是直角的四边形不一定是正方形，所以D错误. 故选D.

在下列命题中，是真命题的是（　　）

A. 两条对角线相等的四边形是矩形

B. 两条对角线互相垂直的四边形是菱形

C. 两条对角线互相平分的四边形是平行四边形

D. 两条对角线互相垂直且相等的四边形是正方形

C 【解析】A、两条对角线相等的平行四边形是矩形，故选项A错误； B、两条对角线互相垂直的平行四边形是菱形，故选项B错误； C、根据平行四边形的判定定理可知两条平行线相互平分的四边形是平行四边形，为真命题，故选项C是正确的； D、两条对角线互相垂直且相等的平行四边形是正方形，故选项D错误； 故选C．

下列命题中，正确的是（　　）

A. 四边相等的四边形是正方形

B. 四角相等的四边形是正方形

C. 对角线垂直的平行四边形是正方形

D. 对角线相等的菱形是正方形

D 【解析】试题分析：根据正方形的判定：对角线相等且互相垂直平分的四边形是正方形，对各个选项进行分析． 【解析】 A，错误，四边相等的四边形也可能是菱形； B，错误，矩形的四角相等，但不是正方形； C，错误，对角线垂直的平行四边形是菱形； D，正确，符合正方形的判定； 故选D．

如图，下列条件之一能使平行四边形ABCD是菱形的为（ ）

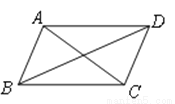
①AC⊥BD ②∠BAD=90° ③AB=BC ④AC=BD

A. ①③ B. ②③ C. ③④ D. ①②③

A 【解析】试题解析： ∵AC⊥BD，四边形ABCD是平行四边形， ∴平行四边形ABCD是菱形，不能推出四边形ABCD是矩形，∴①错误； ∵四边形ABCD是平行四边形， ∴平行四边形ABCD是矩形，∴②正确； ∵AB=BC，四边形ABCD是平行四边形， ∴平行四边形ABCD是菱形，不能推出四边形ABCD是矩形，∴③错误； ∵四边形ABCD是平行四边形...

在四边形ABCD中，AC、BD相交于O，能判定这个四边形是正方形的是（　　）

A. AO=BO=CO=DO，AC⊥BD B. AB∥CD，AC=BD

C. AO=BO，∠A=∠C D. AO=CO，BO=DO，AB=BC

A 【解析】试题分析：根据正方形的判定定理一次分析各项即可判断. A. AO=BO=CO=DO，AC⊥BD，能判定，本选项正确； B. AB∥CD，AC=BD，C. AD∥BC，∠A=∠C，D. AO=CO，BO=CO，AB=BC，均不能判定.