练习册

  • 练习册
  • 试题
    相关习题
     0  321445  321453  321459  321463  321469  321471  321475  321481  321483  321489  321495  321499  321501  321505  321511  321513  321519  321523  321525  321529  321531  321535  321537  321539  321540  321541  321543  321544  321545  321547  321549  321553  321555  321559  321561  321565  321571  321573  321579  321583  321585  321589  321595  321601  321603  321609  321613  321615  321621  321625  321631  321639  366461 

    科目： 来源：2018人教版七年级数学下册练习：第六章达标检测卷 题型：填空题

    算术平方根等于本身的实数是__________.

    0.1 【解析】根据负数没有算术平方根，一个正数的算术平方根只有一个，1和0的算术平方根等于本身，即可得出答案． 【解析】 1和0的算术平方根等于本身. 故答案为：1和0 “点睛”本题考查了算术平方根的知识，注意掌握1和0的算术平方根等于本身．

    查看答案和解析>>

    科目： 来源：2018人教版七年级数学下册练习：第六章达标检测卷 题型：填空题

    化简： =__________.

    －3 【解析】=|3?π|=π?3， 故答案为：π?3.

    查看答案和解析>>

    科目： 来源：2018人教版七年级数学下册练习：第六章达标检测卷 题型：填空题

    的平方根是_______；125的立方根是________.

    ± 5 【解析】∵(±)2=，∴的平方根是±； ∵53=125，∴125的立方根是5. 故答案为：±，5.

    查看答案和解析>>

    科目： 来源：2018人教版七年级数学下册练习：第六章达标检测卷 题型：填空题

    一正方形的边长变为原来的m倍，则面积变为原来的_______倍；一个立方体的体积变为原来的n倍，则棱长变为原来的__________倍.

    m2 【解析】∵正方形的面积=边长×边长，令原正方形的边长为1，则有则×=； 正方体的体积=棱长×棱长×棱长，令原正方体的边长为1，=n， 故答案为：，.

    查看答案和解析>>

    科目： 来源：2018人教版七年级数学下册练习：第六章达标检测卷 题型：填空题

    估计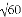的大小约等于____或_____.（误差小于1）

    7 8 【解析】∵49<60<64， ∴7<<8， ∴的大小约等于7或8(误差小于1). 故答案为：7或8.

    查看答案和解析>>

    科目： 来源：2018人教版七年级数学下册练习：第六章达标检测卷 题型：填空题

    若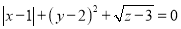，则+ + =________.

    6 【解析】根据非负数的性质列出方程求出x、y、z的值，代入所求代数式计算即可． 【解析】 ∵|x-1|+（y-2）2+=0， ∴x-1=0，y-2=0，z-3=0， ∴x=1，y=2，z=3． ∴x+y+z=1+2+3=6．

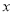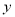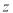    查看答案和解析>>

    科目： 来源：2018人教版七年级数学下册练习：第六章达标检测卷 题型：填空题

    我们知道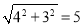，黄老师又用计算器求得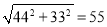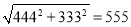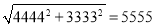： ， ， ，则计算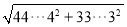： （2001个3，2001个4）=___________.

    2011个5 【解析】∵， ， …， ∴ (2001个3, 2001个4)=555…5(2001个5). 故答案为：555…5(2001个5).

    查看答案和解析>>

    科目： 来源：2018人教版七年级数学下册练习：第六章达标检测卷 题型：解答题

    求下列各数的平方根和算术平方根：（1）1； （2）；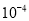

    （1） ±1，1；（2）±， . 【解析】试题分析：（1）根据平方运算，可得平方根、算术平方根； （2）根据负整指数幂，可得正整指数幂，根据平方运算，可得平方根、算术平方根． 试题解析：（1）∵(±1)2=1， ∴±=±1， =1； （2）∵(±)2=， ∴±=±， =，

    查看答案和解析>>

    科目： 来源：2018人教版七年级数学下册练习：第六章达标检测卷 题型：解答题

    求下列各数的立方根：

    （1）；

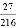    （2）-10-6；

    （1） （2）-10-2 【解析】试题分析：（1）直接利用立方根的定义求出即可； （2）直接利用立方根的定义求出即可． 试题解析：（1）=， ∵()3=，所以的立方根是； （2）∵()3=，所以的立方根是.

    查看答案和解析>>

    科目： 来源：2018人教版七年级数学下册练习：第六章达标检测卷 题型：解答题

    化简：

    （1） ；

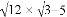    （2）

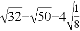
    （1）1（2）-2 【解析】试题分析：（1）根据二次根式的乘法法则运算； （2）先把各二次根式化为最简二次根式，然后合并即可. 试题解析：(1)原式==6?5=1； （2）原式=4?5?=?.

    查看答案和解析>>

    同步练习册答案