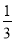相关习题
0 321452 321460 321466 321470 321476 321478 321482 321488 321490 321496 321502 321506 321508 321512 321518 321520 321526 321530 321532 321536 321538 321542 321544 321546 321547 321548 321550 321551 321552 321554 321556 321560 321562 321566 321568 321572 321578 321580 321586 321590 321592 321596 321602 321608 321610 321616 321620 321622 321628 321632 321638 321646 366461
科目:
来源:甘肃省平凉市2017-2018学年八年级(上)期中数学试卷
题型:填空题
已知一个多边形的内角和与外角和的差为1080°,则这个多边形是______边形.
十.
【解析】根据题意,得(n﹣2)•180=1080+360,解得:n=10.所以这个多边形是十边形.
查看答案和解析>>
科目:
来源:甘肃省平凉市2017-2018学年八年级(上)期中数学试卷
题型:解答题
如图,AB∥CD,∠A=38°,∠C=80°,求∠M.

42°.
【解析】试题分析:根据平行线的性质和三角形的一个外角等于和它不相邻的两个内角的和解答即可.
试题解析:
∵AB∥CD,∠C=80°,
∴∠MEB=∠C=80°,
∵∠A=38°,∠MEB=∠A+∠M,
∴∠M=80°﹣38°=42°.
查看答案和解析>>
科目:
来源:甘肃省平凉市2017-2018学年八年级(上)期中数学试卷
题型:解答题
(8分)如图,∠A=90°,∠B=21°,∠C=32°,求∠BDC的度数。
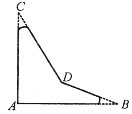
【解析】
如图,连接AD并延长AD至点E
因为∠BDE=∠1+∠B ,∠CDE=∠2+∠C
所以∠BDC=∠BDE+∠CDE=∠1+∠2+∠B+∠C
=∠BAC+∠B+∠C
因为∠A=90°,∠B=21°,∠C=32°
所以∠BDC=90°+21°+32°=143°.
【解析】
试题分析:连接AD并延长AD至点E,根据三角形的外角性质求出∠BDE=∠1+...
查看答案和解析>>
科目:
来源:甘肃省平凉市2017-2018学年八年级(上)期中数学试卷
题型:解答题
如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.

18°.
【解析】试题分析:根据三角形的内角和定理与∠C=∠ABC=2∠A,即可求得△ABC三个内角的度数,再根据直角三角形的两个锐角互余求得∠DBC的度数.
试题解析:∵∠C=∠ABC=2∠A,
∴∠C+∠ABC+∠A=5∠A=180°,
∴∠A=36°.
则∠C=∠ABC=2∠A=72°.
又BD是AC边上的高,
则∠DBC=90°-∠C=18°.
查看答案和解析>>
科目:
来源:甘肃省平凉市2017-2018学年八年级(上)期中数学试卷
题型:解答题
如图,B、F、E、C四点在同一条直线上,AB=CD,AE=DF,CE=FB,判断∠B与∠C的关系,并证明.

∠B=∠C.
【解析】试题分析:根据已知条件证明△ABE≌△DCF,根据全等三角形的性质即可得结论.
试题解析:
结论:∠B=∠C.
理由:∵CE=BF,
∴CE+EF=EF+BF,即CF=BE,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SSS),
∴∠B=∠C.
查看答案和解析>>
科目:
来源:甘肃省平凉市2017-2018学年八年级(上)期中数学试卷
题型:解答题
如图,∠B=42°,∠A+10°=∠1,∠ACD=64°,证明:AB∥CD.
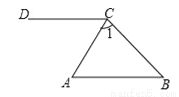
答案见解析.
【解析】试题分析:在△ABC中,∠B=42°,根据三角形的内角和定理可得∠A+∠1=180°﹣42°=138°,又∠A+10°=∠1可以求出∠A的大小,从而得∠A=∠ACD,再根据内错角相等,两直线平行,即可证出结论.
试题解析:
证明:在△ABC中,∠A+∠B+∠1=180°,∠B=42°,
∴∠A+∠1=138°,
又∵∠A+10°=∠1,
∴...
查看答案和解析>>
科目:
来源:甘肃省平凉市2017-2018学年八年级(上)期中数学试卷
题型:解答题
如图:已知AB,CD相交于点O,且AB=DC,AC=DB,求证:∠A=∠D.

答案见解析.
【解析】试题分析:连接BC,利用SSS证明△ABC≌△DCB,根据全等三角形的性质即可得结论.
试题解析:
证明:连结BC,
在△ABC和△DCB中,
,
∴△ABC≌△DCB(SSS),
∴∠A=∠D.
查看答案和解析>>
科目:
来源:甘肃省平凉市2017-2018学年八年级(上)期中数学试卷
题型:解答题
如图,六边形ABCDEF中,AF∥CD,AB∥DE,∠A=140°,∠B=100°,∠E=90°,求:∠C、∠D、∠F的度数.
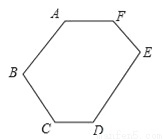
∠C=120°,∠CDE=140°,∠F=130°.
【解析】试题分析:连接AD,由AF∥CD得出∠FAD=∠ADC,由AB∥DE得出∠BAD=∠ADE,故可得出∠CDE=∠BAF,∠FAD+∠ADE=∠ADC+∠BAD=∠BAF,再由四边形内角和定理即可得出∠F与∠C的度数.
试题解析:
连接AD,
∵AF∥CD,
∴∠FAD=∠ADC.
∵AB∥DE,
...
查看答案和解析>>
科目:
来源:甘肃省平凉市2017-2018学年八年级(上)期中数学试卷
题型:解答题
已知如图,在△ABC中,AD、AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°
1.求∠DAE的度数。
2.试写出∠DAE与∠B、∠C之间关系?(不必证明)
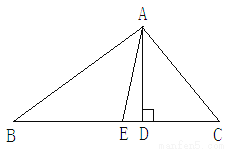
1.∵∠B=30°,∠C=50°,
∴∠BAC=180°-30°-50°=100°.
∵AE是∠BAC的平分线,
∴∠BAE=50°.(5分)
在Rt△ABD中,∠BAD=90°-∠B=60°,
∴∠DAE=∠BAD-∠BAE=60°-50=10°;(12分)
2.∠C-∠B=2∠DAE.(14分)
【解析】略
查看答案和解析>>
科目:
来源:湖北省鄂州市2017-2018学年七年级(上)期中数学试卷
题型:单选题
﹣3的相反数是( )
A. ﹣3 B. ﹣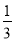 C. 3 D.
C. 3 D. 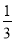
C
【解析】根据一个数的相反数就是在这个数前面添上“﹣”号,可得﹣3的相反数是3,故选C.
查看答案和解析>>









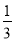 C. 3 D.
C. 3 D.