
��ͼ���ڡ�ABC�У���C=��ABC=2��A��BD��AC���ϵĸߣ����DBC�Ķ�����

 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2018�˽̰����꼶��ѧ�²���ϰ�������´����� ���ͣ������
һ�����εı߳���Ϊԭ����m�����������Ϊԭ����_______����һ��������������Ϊԭ����n�������ⳤ��Ϊԭ����__________��.
m2 ���������������ε����=�߳����߳�����ԭ�����εı߳�Ϊ1���������=�� ����������=�ⳤ���ⳤ���ⳤ����ԭ������ı߳�Ϊ1��=n�� �ʴ�Ϊ����.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ������
�ס������ҳ�������ͬ�ļ۸����ͬ������Ʒ����Ϊ�������˿ͣ������Ƴ���ͬ���Żݷ������ڼ׳����ۼƹ�����Ʒ����400Ԫ�������ְ�ԭ�������Żݣ����ҳ��й�����Ʒֻ��ԭ�۵İ����Żݣ���˿��ۼƹ���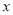 Ԫ��
Ԫ��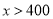 ��
��
��1���ú�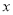 �Ĵ���ʽ�ֱ��ʾ�˿������ҳ��й��������ķ��á�
�Ĵ���ʽ�ֱ��ʾ�˿������ҳ��й��������ķ��á�
��2����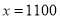 ʱ���ԱȽϹ˿͵��ļҳ��й�������Żݡ�
ʱ���ԱȽϹ˿͵��ļҳ��й�������Żݡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
��A��B�������ζ���ʽ����A+Bһ���ǣ�������
A. ���ζ���ʽ
B. �������������Ķ���ʽ����ʽ
C. ���ζ���ʽ
D. ���ε���ʽ
B ������������A��B�������ζ���ʽ���ϲ���Ķ���ʽ�Ĵ������ܸ������Σ�����A+B���������ζ���ʽ��Ҳ�����ǵ���ʽ����ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡƽ����2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
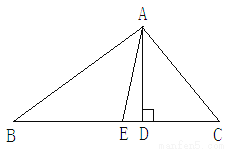
��֪��ͼ���ڡ�ABC�У�AD��AE�ֱ��ǡ�ABC�ĸߺͽ�ƽ���ߣ�����B=30�㣬��C=50��
1.���DAE�Ķ�����
2.��д����DAE���B����C֮���ϵ��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡƽ����2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��һ��n���ε�һ����Dz�����40�㣬���������ο�����______��
���ű��Σ� ����������360��40=9�� ��ÿ����Ƕ�����40����������Ϊ���ű��Σ� ����������n���ε�ÿһ����Ƕ�������40�㣬 �����������ұ������ٵĶ����Ϊ���ű��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡƽ����2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
������ε�һ�����������7���Խ��ߣ���˶���ε��ڽǺ�����Ǻ͵ģ�������
A. 4�� B. 5�� C. 6�� D. 3��
A ���������߹�����ε�һ�����㹲��7���Խ��ߣ� ��ö���α���Ϊ10�� �ࣨ10��2��•180��=1440�㣬 ���������ε��ڽǺ�Ϊ1440�㣬 �֡߶���ε���Ǻ�Ϊ360�㣬 ��1440��360=4�� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�˽̰��ϲ��24�� Բ ��Ԫ���Ծ� ���ͣ������
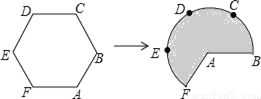
��ͼ�����߳�Ϊ3������������˿��ABCDEF����Ϊ�Ե�AΪԲ�ģ�ABΪ�뾶�����Σ�������˿�Ĵ�ϸ��������������AFB����Ӱ���֣������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�˽̰��ϲ��23�� ��ת ��Ԫ���Ծ� ���ͣ������
��ͼ,��������ABC�ƶ���B��ʱ�뷽����ת���ȵ���A1B1C1��λ��,AB��A1C1�ཻ�ڵ�D,AC��A1C1��BC1�ֱ��ڵ�E. F.

(1)��֤����BCF�ա�BA1D.
(2)����C=����ʱ,�ж��ı���A1BCE����״��˵�����ɡ�
(1)֤��������(2)�ı���A1BCE������ �������������������1�����ݵ��������ε����ʵõ�AB=BC����A=��C������ת�����ʵõ�A1B=AB=BC����A=��A1=��C����A1BD=��CBC1������ȫ�������ε��ж������õ���BCF�ա�BA1D����2������ת�����ʵõ���A1=��A������ƽ�ǵĶ���õ���DEC=180�㩁���������ı��ε��ڽǺ͵õ���ABC=360�㩁��A1����C����A1EC=...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com