相关习题
0 321455 321463 321469 321473 321479 321481 321485 321491 321493 321499 321505 321509 321511 321515 321521 321523 321529 321533 321535 321539 321541 321545 321547 321549 321550 321551 321553 321554 321555 321557 321559 321563 321565 321569 321571 321575 321581 321583 321589 321593 321595 321599 321605 321611 321613 321619 321623 321625 321631 321635 321641 321649 366461
科目:
来源:2017-2018学年九年级数学人教版上册:第24章 圆 单元测试卷
题型:填空题
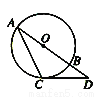
如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠D=40°,则∠A的度数为______.
25°
【解析】连接OC,∵CD是切线,∴∠OCD=90°,∵∠D=40°,∴∠COD=90°-∠D=50°,
∵OA=OC,∴∠A=∠OCA,∵∠A+∠OCA=∠COD,∴∠A=25°,
故答案为:25°.
查看答案和解析>>
科目:
来源:2017-2018学年九年级数学人教版上册:第24章 圆 单元测试卷
题型:填空题
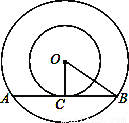
如图,两同心圆的大圆半径长为5cm,小圆半径长为3cm,大圆的弦AB与小圆相切,切点为C,则弦AB的长是 ______ .
8cm
【解析】试题解析:∵AB是⊙O切线,
∴OC⊥AB,
∴AC=BC,
在Rt△BOC中,∵∠BCO=90°,OB=5,OC=3,
∴BC==4(cm),
∴AB=2BC=8cm.
查看答案和解析>>
科目:
来源:2017-2018学年九年级数学人教版上册:第24章 圆 单元测试卷
题型:填空题
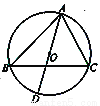
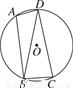
如图,⊙O是△ABC的外接圆,直径AD=4,∠ABC=∠DAC,则AC长为________.
2
【解析】试题解析:连接CD,如图所示:
∵∠B=∠DAC,
∴,
∴AC=CD,
∵AD为直径,
∴∠ACD=90°,
在Rt△ACD中,AD=4,
∴AC=CD=AD=×4=.
查看答案和解析>>
科目:
来源:2017-2018学年九年级数学人教版上册:第24章 圆 单元测试卷
题型:填空题
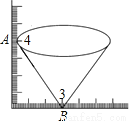
一个圆锥形漏斗,某同学用三角波测得其高度的尺寸如图所示,则该圆锥形漏斗的侧面积为 ______ .
15π
【解析】试题解析:圆锥的母线长=,
所以该圆锥形漏斗的侧面积=×2π×3×5=15π.
查看答案和解析>>
科目:
来源:2017-2018学年九年级数学人教版上册:第24章 圆 单元测试卷
题型:填空题
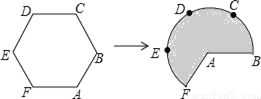
如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为_____.
18
【解析】试题分析:∵正六边形ABCDEF的边长为3,∴AB=BC=CD=DE=EF=FA=3,∴弧BAF的长=3×6﹣3﹣3═12,∴扇形AFB(阴影部分)的面积=×12×3=18.故答案为:18.
查看答案和解析>>
科目:
来源:2017-2018学年九年级数学人教版上册:第24章 圆 单元测试卷
题型:填空题
如图,圆O的直径AB为13cm,弦AC为5cm,∠ACB的平分线圆O于D,则CD长是_______cm
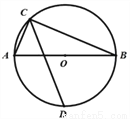
【解析】试题分析:首先作DF⊥CA,交CA的延长线于点F,作DG⊥CB于点G,连接DA,DB.由CD平分∠ACB,根据角平分线的性质得出DF=DG,由HL证明△AFD≌△BGD,得出CF的长,又△CDF是等腰直角三角形,从而求出CD的长.
【解析】
作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB.
∵CD平分∠ACB,
∴∠ACD=∠BCD
∴D...
查看答案和解析>>
科目:
来源:2017-2018学年九年级数学人教版上册:第24章 圆 单元测试卷
题型:填空题
如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=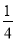 AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=
AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=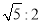 .当边AD或BC所在的直线与⊙O相切时,AB的长是 .
.当边AD或BC所在的直线与⊙O相切时,AB的长是 .
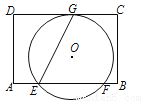
4或12.
【解析】试题分析:边AB所在的直线不会与⊙O相切;边BC所在的直线与⊙O相切时,
如图,过点G作GN⊥AB,垂足为N,∴EN=NF,
又∵EG:EF=,∴EG:EN=,
又∵GN=AD=8,∴设EN= ,则GE= ,
根据勾股定理得: ,解得:x=4,GE=,
设⊙O的半径为,由,得: ,∴.∴OK=NB=5,∴EB=9,
又AE=AB,∴AB...
查看答案和解析>>
科目:
来源:2017-2018学年九年级数学人教版上册:第24章 圆 单元测试卷
题型:解答题
如图,已知⊙O中直径AB与弦AC的夹角为30°,过点C作⊙O的切线交AB的延长线于点D,OD=30cm.求直径AB的长.
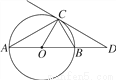
30cm.
【解析】试题分析:先求出∠COD,根据切线的性质知∠OCD=90°,从而求出∠D,根据含30度角的直角三角形性质求出OC,即可求出答案.
试题解析:∵AB为⊙O的直径,∴∠ACB=90°,
∵∠BAC=30°,∴在△ABC中,∠ABC=90°-∠BAC=60°,
∵OB=OC,∴△OBC为等边三角形,∴∠BOC=60°,
又∵CD为⊙的切线,∴∠OCD=9...
查看答案和解析>>
科目:
来源:2017-2018学年九年级数学人教版上册:第24章 圆 单元测试卷
题型:解答题
如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
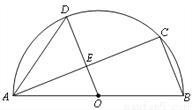
(1) ∠CAD=35° (2) DE=
【解析】试题分析:
(1)由AB是直径可得∠C=90°,由OD∥BC可得∠AOD=∠B=70°,∠OEA=90°,再由OA=OD,可得∠D=∠DAO=,最后在Rt△ADE中可求得∠CAD;
(2)由(1)中∠OEA=90°可得OE⊥AC,从而得到AE=AC=1.5,再由AB=4可得AO=2,就可在Rt△AEO中由勾股定理求得OE,最后由O...
查看答案和解析>>
科目:
来源:2017-2018学年九年级数学人教版上册:第24章 圆 单元测试卷
题型:解答题
如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求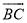 的长.
的长.
(1)证明见解析;(2)π.
【解析】试题分析: 根据圆内接四边形的对角互补,∠DCB+∠BAD=180°,即可求出
的度数,得出,根据等角对等边即可证明.
求出的度数,根据弧长公式计算即可.
试题解析:
证明:∵四边形ABCD内接于圆O,
∴∠DCB+∠BAD=180°.
∵∠BAD=105°,
∴∠DCB=180°-105°=75°.
∵∠...
查看答案和解析>>







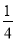 AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=
AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=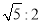 .当边AD或BC所在的直线与⊙O相切时,AB的长是 .
.当边AD或BC所在的直线与⊙O相切时,AB的长是 .


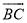 的长.
的长.