
科目: 来源:人教版九年级下册 期中测试卷 题型:填空题
将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=6,BC=8.若以点B′,F,C为顶点的三角形与△ABC相似,则BF的长度是______
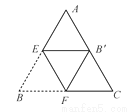
查看答案和解析>>
科目: 来源:人教版九年级下册 期中测试卷 题型:解答题
如图,反比例函数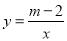 的图象的一支在平面直角坐标系中的位置如图所示,根据图象回答下列问题:
的图象的一支在平面直角坐标系中的位置如图所示,根据图象回答下列问题:
(1)图象的另一支在第 象限;在每个象限内,y随x的增大而 ;
(2)若此反比例函数的图象经过点(-2,3),求m的值.点A(-5,2)是否在这个函数图象上?点B(-3,4)呢?
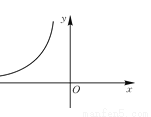
查看答案和解析>>
科目: 来源:人教版九年级下册 期中测试卷 题型:解答题
一定质量的氧气,其密度ρ(kg/m3)是它的体积v (m3)的反比例函数.当V=10m3 时ρ=1.43kg/m3.
(1)求ρ与v的函数关系式;
(2)求当V=2m3时,氧气的密度.
(1);(2) 【解析】 试题分析:(1)设ρ与v的函数关系式为,根据V=10m3 时ρ=1.43kg/m3即得结果; (2)把V=2m3代入(1)中的函数关系式即可求得结果. (1)设ρ与v的函数关系式为, 由V=10m3 时ρ=1.43kg/m3得 答:ρ与v的函数关系式为; (2)当V=2m3时, 答:氧气的密度为查看答案和解析>>
科目: 来源:人教版九年级下册 期中测试卷 题型:解答题
如图,已知梯形ABCD,AB∥DC,△AOB的面积等于9,△AOD的面积等于6,AB=7,求CD的长.
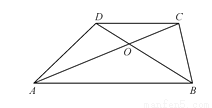
查看答案和解析>>
科目: 来源:人教版九年级下册 期中测试卷 题型:解答题
为了估算河的宽度,我们可以在河对岸的岸边选定一个目标作为点A,再在河的这一边选点B和点C,使AB⊥BC,然后再选点E,使EC⊥BC,确定BC与AE的交点为D,如图.测得BD=120米,DC=60米,EC=50米,你能求出两岸之间AB的大致距离吗?
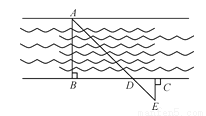
查看答案和解析>>
科目: 来源:人教版九年级下册 期中测试卷 题型:解答题
如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.
(1)如果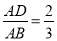 ,DE=6,求边BC的长;
,DE=6,求边BC的长;
(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
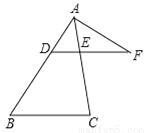
查看答案和解析>>
科目: 来源:人教版九年级下册 期中测试卷 题型:解答题
如图,在平面直角坐标系中,直线AB与函数y=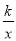 (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=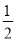 OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.
查看答案和解析>>
科目: 来源:人教版九年级下册 期中测试卷 题型:解答题
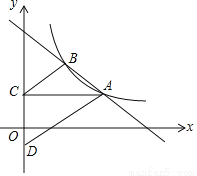
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
(1) t=1或 ;(2) 【解析】试题分析: (1)由∠B是△BPQ与△ABC的公共角,可知,若两三角形相似,存在两种情况:①△BPQ∽△BAC;②△BPQ∽△BCA;分这两种情况结合相似三角形的性质和题意即可解得对应的t的值; (2)如图1,过P作PM⊥BC于点M,AQ,CP交于点N,由题意可知:当AQ⊥CP时,△ACQ∽△CMP,由相似三角形的性质列出比例式即可解得对应的t...查看答案和解析>>
科目: 来源:人教版九年级下册 期中测试卷 题型:解答题
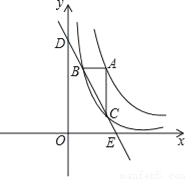
如图,点A在函数y= (x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=
(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y= 图象于点B,C,直线BC与坐标轴的交点为D,E.
图象于点B,C,直线BC与坐标轴的交点为D,E.
(1)当点C的横坐标为1时,求点B的坐标;
(2)试问:当点A在函数y= (x>0)图象上运动时,△ABC的面积是否发生变化?若不变,请求出△ABC的面积,若变化,请说明理由.
(x>0)图象上运动时,△ABC的面积是否发生变化?若不变,请求出△ABC的面积,若变化,请说明理由.
(3)试说明:当点A在函数y= (x>0)图象上运动时,线段BD与CE的长始终相等.
(x>0)图象上运动时,线段BD与CE的长始终相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com