相关习题
0 321493 321501 321507 321511 321517 321519 321523 321529 321531 321537 321543 321547 321549 321553 321559 321561 321567 321571 321573 321577 321579 321583 321585 321587 321588 321589 321591 321592 321593 321595 321597 321601 321603 321607 321609 321613 321619 321621 321627 321631 321633 321637 321643 321649 321651 321657 321661 321663 321669 321673 321679 321687 366461
科目:
来源:人教版七年级下册数学第五章相交线与平行线单元检测卷
题型:填空题
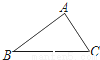
如图:△ABC中,∠A的同旁内角是________ .
∠B和∠C
【解析】当AB为截线时,∠A与∠B为同旁内角;当AC为截线时,∠A与∠C为同旁内角.
故答案为∠B和∠C.
查看答案和解析>>
科目:
来源:人教版七年级下册数学第五章相交线与平行线单元检测卷
题型:填空题
如图,AB//CD,∠CDE=119º,GF交∠DEB的平分线EF于F,∠AGF=130º,则∠F= 。
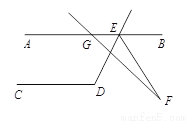
9.5º或9º30´.
【解析】试题分析:已知AB//CD,∠CDE=119º,根据平行线的性质可得∠CDE=∠DEB=119º,∠AED=180º—119º=61º;由EF平分∠DEB可得∠DEF=∠DEB=59.5º,所以∠GEF=∠DEF+∠AED=59.5º+61º=120.5º.再由三角形的一个外角等于与它不相邻的两个内角的和可得∠F=∠AGF—∠G...
查看答案和解析>>
科目:
来源:人教版七年级下册数学第五章相交线与平行线单元检测卷
题型:解答题
如果∠A与∠B的两条边分别平行,其中∠A=(x+30)°;∠B =(3x-10)°,那么∠A的度数为________
50°或70°
【解析】(1)如图(1)
由题意知:AM//BE,AN//BF,
∴∠A=∠1=(x+30)°,∠2+∠B=180°
又∠1=∠2,∴∠2=∠A=(x+30)°,
又∠B=(3x-10)°,
∴ ,解得x=40,
∴∠A=(40+30)°=70°.
(2)如图(2,),
由题意知:AM//BE,AN//BF,
∴∠1=∠A...
查看答案和解析>>
科目:
来源:人教版七年级下册数学第五章相交线与平行线单元检测卷
题型:填空题
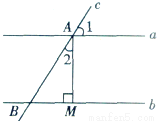
如图所示,直线a∥b,直线c与直线a,b分别相交于点A、点B,AM⊥b,垂足为点M,若∠l=58°,则∠2= ___________ .
32°
【解析】根据“在同一平面内,垂直于两条平行线中的一条直线,那么必定垂直于另一条直线”推知AM⊥a;然后由平角是180°、∠1=58°来求∠2的度数即可.
【解析】
∵直线a∥b,AM⊥b,
∴AM⊥a(在同一平面内,垂直于两条平行线中的一条,那么必定垂直于另一条);
∴∠2=180°-90°-∠1;
∵∠1=58°,
∴∠2=32°.
故答案是:...
查看答案和解析>>
科目:
来源:人教版七年级下册数学第五章相交线与平行线单元检测卷
题型:填空题
如图,请写出能判定CE∥AB的一个条件_________.
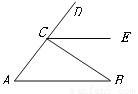
∠EBC= ∠B(答案不唯一)
【解析】试题分析:能判定CE∥AB的,判别两条直线平行的方法有:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.因而可以判定的条件是:∠DCE=∠A或∠ECB=∠B或∠A+∠ACE=180°.
【解析】
能判定CE∥AB的一个条件是:∠DCE=∠A或∠ECB=∠B或∠A+∠ACE=180°.
故答案为:∠DCE=∠A(答...
查看答案和解析>>
科目:
来源:人教版七年级下册数学第五章相交线与平行线单元检测卷
题型:填空题
如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED=________.
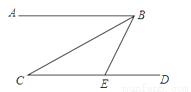
68°
【解析】如图,
∵BC平分∠ABE,∴∠1=∠2,
又∵AB∥CD,∴∠C=∠1,
∴∠1=∠2=∠C=34°,
又∠BED是△BCE的外角,
∴∠BED=∠2+∠C=68°.
故答案为68°.
查看答案和解析>>
科目:
来源:人教版七年级下册数学第五章相交线与平行线单元检测卷
题型:解答题
如图,已知AD⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°,那么BC⊥AB,说明理由。

如图:
∵DE,CE分别平分∠ADC,∠BCD
∴∠ADC=2∠1 ∠DCB=2∠2 (3分)
∵∠1+∠2=90°
∴∠ADC+∠BCD=180°
∴AD∥BC (6分)
∴∠A+∠B=180°
∵BC⊥AB∴∠A=90°
∴∠CBE=90°
∴CB⊥AB (8分)
【解析】利用两直线平行的性质和判定定理来求。
查看答案和解析>>
科目:
来源:人教版七年级下册数学第五章相交线与平行线单元检测卷
题型:解答题
如图,直线a、b被直线l所截,已知∠1=40°,试求∠2的同位角及同旁内角的度数.
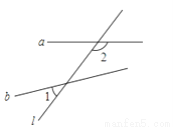
∠2的同位角是140°,∠2的同旁内角是40°.
【解析】试题分析:
首先要确定∠2的同位角、同旁内角是哪一个:因l为截线,这两个角与∠2必然位于l的同旁,即直线l的右边的∠3与∠4;再根据对顶角性质及补角定理,就可求出两角大小.
【解析】
如图,
∵∠1=40°,
∴∠4=∠1=40°,∠3=180°﹣∠1=140°,
即∠2的同位角是140°,∠2的同旁内...
查看答案和解析>>
科目:
来源:人教版七年级下册数学第五章相交线与平行线单元检测卷
题型:解答题
已知:如图,∠1=120°,∠C=60°,判断AB与CD是否平行?为什么?
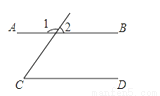
见解析
【解析】试题分析:
根据平行线判定定理,要判断两直线是否平行,需找到是否有相关的同位角、内错角相等,或是同旁内角互补,由图可知只要判断出∠C与∠2这一对同位角是否相等即可.
【解析】
AB与CD是平行.
理由如下:∵∠1=120°, ∴∠2=180°﹣∠1=60°.
又∵∠C=60°,
∴∠2=∠C,
∴AB∥CD.
查看答案和解析>>
科目:
来源:人教版七年级下册数学第五章相交线与平行线单元检测卷
题型:解答题
已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.
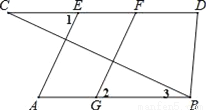
(2)25°
【解析】试题分析:(1)求出AE∥GF,求出∠2=∠A=∠1,根据平行线的判定推出即可;
(2)根据平行线的性质得出∠D+∠CBD+∠3=180°,求出∠3,根据平行线的性质求出∠C即可.
试题解析:(1)证明:
∵AE⊥BC,FG⊥BC,
∴∠4=∠5=90o.
∴AE∥FG.
∴∠2=∠A.
∵∠1=∠2,
∴∠1=∠A.
...
查看答案和解析>>