练习册

  • 练习册
  • 试题
    相关习题
     0  321520  321528  321534  321538  321544  321546  321550  321556  321558  321564  321570  321574  321576  321580  321586  321588  321594  321598  321600  321604  321606  321610  321612  321614  321615  321616  321618  321619  321620  321622  321624  321628  321630  321634  321636  321640  321646  321648  321654  321658  321660  321664  321670  321676  321678  321684  321688  321690  321696  321700  321706  321714  366461 

    科目： 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：填空题

    若关于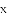的一元二次方程(m-1)x2-4x+1=0有两个不相等的实数根，则m的取值范围为_____________．

    且 【解析】试题解析: ∵一元二次方程有两个不相等的实数根， ∴m?1≠0且△=16?4(m?1)>0，解得m<5且m≠1， ∴m的取值范围为m<5且m≠1. 故答案为:m<5且m≠1.

    查看答案和解析>>

    科目： 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：填空题

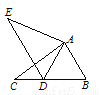
    如图，在△ABC中，AB=4，BC=7，∠B=60°，将△ABC绕点A按顺时针旋转一定角度得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为__________．

    3 【解析】试题解析: 由旋转的性质可得：AD=AB， ∴△ABD是等边三角形， ∴BD=AB， ∵AB=4，BC=7， ∴CD=BC?BD=7?4=3. 故答案为：3.

    查看答案和解析>>

    科目： 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：填空题

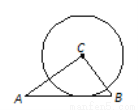
    如图，在△ABC中，AB=5，BC=3，AC=4，以点C为圆心的圆与AB相切，则⊙C的半径为____________．

    【解析】试题解析: 在△ABC中， ∵AB=5，BC=3，AC=4， 如图：设切点为D，连接CD， ∵AB是C的切线， ∴CD⊥AB， ∴AC?BC=AB?CD， 即 ∴的半径为 故答案为:

    查看答案和解析>>

    科目： 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：填空题

    有一个二次函数的图象，三位同学分别说了它的一些特点：

    甲：与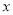轴只有一个交点；

    乙：对称轴是直线；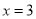

    丙：与y轴的交点到原点的距离为3．

    满足上述全部特点的二次函数的解析式为______________________．

    或 【解析】试题解析: ∵二次函数的对称轴为直线x=3， ∴k=3， ∴二次函数的解析式为 ∵与y轴的交点到原点的距离为3， ∴与y轴交于点(0,3)或(0,?3)， 把(0,3)代入得， 把(0,?3)代入得， ∴解析式为： 或. 故答案为： 或.

    查看答案和解析>>

    科目： 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：解答题

    解一元二次方程： ．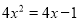

    【解析】试题分析:用直接开方法解方程即可. 试题解析: 原方程可化为： ， ∴， 解得： ．

    查看答案和解析>>

    科目： 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：解答题

    已知抛物线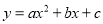经过点A（1，0），B（-1，0），C（0，-2）．求此抛物线的函数解析式和顶点坐标．

    抛物线顶点坐标为（0，-2） 【解析】试题分析: 利用待定系数法即可求出二次函数解析式，化为顶点式即可求出抛物线的顶点坐标． 试题解析: 把点A（1，0）、B（-1，0）、C（0，-2）的坐标, 分别代入得： ， 解得： ， ∴二次函数的解析式为． ∴抛物线顶点坐标为（0，-2）．

    查看答案和解析>>

    科目： 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：解答题

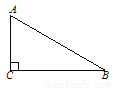
    如图，在Rt△ABC中，∠ACB＝90°，∠ABC＝30°，AC=3．

    (1)以BC边上一点O为圆心作⊙O，使⊙O分别与AC、AB都相切 (要求：尺规作图，保留作图痕迹，不写作法) ；

    (2)求⊙O的面积．

    （1）图形见解析（2）3π 【解析】试题分析: 作的平分线即可. 求出的半径,即可求出的面积. 试题解析: （1）如图所示：⊙O为所求的图形． （2）在Rt△ABC中， ∵∠ABC＝30°， ∴∠CAB＝60°， ∵AO平分∠CAB，∴∠CAO＝30°， 设，则， ∵在Rt△ACO中， ， ∴, 解得： 或（负值不合题意，舍去...

    查看答案和解析>>

    科目： 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：解答题

    车辆经过润扬大桥收费站时，4个收费通道 A．B、C、D中，可随机选择其中的一个通过．

    （1）一辆车经过此收费站时，选择 A通道通过的概率是 ；

    （2）求两辆车经过此收费站时，选择不同通道通过的概率．

    （1）；（2）． 【解析】试题分析：（1）根据概率公式即可得到结论； （2）画出树状图即可得到结论． 试题解析：（1）选择 A通道通过的概率=， 故答案为： ； （2）设两辆车为甲，乙，如图，两辆车经过此收费站时，会有16种可能的结果，其中选择不同通道通过的有12种结果，∴选择不同通道通过的概率==．

    查看答案和解析>>

    科目： 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：解答题

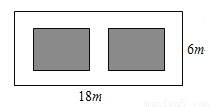
    如图，某小区有一块长为18米，宽为6米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为60米2，两块绿地之间及周边留有宽度相等的人行通道．求人行通道的宽度．

    人行通道的宽度为1米 【解析】试题分析：设人行道的宽度为x米，根据矩形绿地的面积之和为60米2，列出一元二次方程． 设人行道的宽度为x米(0

    查看答案和解析>>

    科目： 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：解答题

    正方形ABCD的边长为3，E，F分别是AB，BC边上的点，且∠EDF＝45°，将△DAE绕点D逆时针旋转90°，得到△DCM.

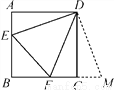
    (1)求证：EF＝FM；

    (2)当AE＝1时，求EF的长．

    （1）详见解析；（2）. 【解析】试题分析：（1）由旋转的性质可知，DE=DM，∠EDM=90°，因为∠EDF=45°，所以∠FDM=∠EDM=45°，通过证明△DEF≌△DMF得到EF=MF； （2）设EF=MF=x，则BF=4-x，BE=2，在Rt△EBF中，由勾股定理得到关于x的等式，解得x的值即可． 试题解析：（1）证明：∵△DAE逆时针旋转90°得到△DCM， ∴...

    查看答案和解析>>

    同步练习册答案