
科目: 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:填空题
一个底面直径是80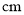 ,母线长为
,母线长为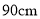 的圆锥的侧面展开图的圆心角的度数为______ 。
的圆锥的侧面展开图的圆心角的度数为______ 。
查看答案和解析>>
科目: 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:填空题
已知点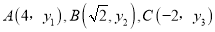 都在二次函数
都在二次函数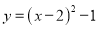 的图象上,则y1, y2 , y3的大小关系是______ 。
的图象上,则y1, y2 , y3的大小关系是______ 。
查看答案和解析>>
科目: 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:填空题
如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数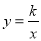 的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
查看答案和解析>>
科目: 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:解答题
用适当的方法解下列方程。
(1)3x(x+3)=2(x+3)
(2)2x2?4x?3=0.
(1)x1=?3,x2= (2) 【解析】试题分析:第小题用因式分解法,第小题用公式法. 试题解析::(1)3x(x+3)-2(x+3)=0, (x+3)(3x-2)=0, 或 (2) ∴ ∴x1=1+,x2=1-.查看答案和解析>>
科目: 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:解答题
如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
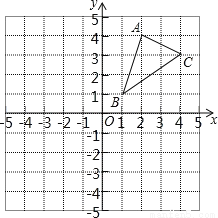
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90?后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).
(4)在x轴上有一点P,PA+PB的值最小,请直接写出点P的坐标
(1)根A1(2,?4),B1(1,?1),C1(4,?3)(2)图形见解析(3) (4)(1.2,0) 【解析】试题分析:(1)利用关于x轴对称点的横坐标相等,纵坐标互为相反数可先找出点A1、B1、C1的坐标,然后画出图形即可; (2)利用旋转的性质可确定出点A2、C2的坐标; (3)先求出BC的长,然后利用弧长公式进行计算即可; (4)连接A1B,与x轴相交于点P,则此...查看答案和解析>>
科目: 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:解答题
为了预防“感冒”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后y与x成反比例如图。现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中提供的信息,解答下列问题:
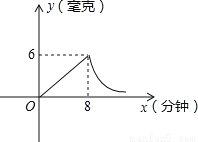
(1)药物燃烧时,y关于x的函数关系式为___,自变量x的取值范围是___;药物燃烧后y关于x的函数关系式为___.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过___分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病毒,那么此次消毒有效吗?为什么?
(1)药物燃烧时y关于x的函数关系式为y=x(0?x?8)药物燃烧后y关于x的函数关系式为y= (x>8)(2)从消毒开始,至少需要30分钟后学生才能进入教室(3)这次消毒是有效的 【解析】试题分析:(1)药物燃烧时,设出y与x之间的解析式y=k1x,把点(8,6)代入即可,从图上读出x的取值范围;药物燃烧后,设出y与x之间的解析式,把点(8,6)代入即可; (2)把y=1.6代入反比...查看答案和解析>>
科目: 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:解答题
如图,已知A(?4,2)、B(a,?4)是一次函数y=kx+b的图象与反比例函数 的图象的两个交点;
的图象的两个交点;

(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(1)反比例函数的解析式为,一次函数的解析式为y=-x-2(2)-4查看答案和解析>>
科目: 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:解答题
如图,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一点O,使OB=OC,以点O为圆心,OB为半径作圆,过点C作CD∥AB交⊙O于点D,连接BD.
(1)猜想AC与⊙O的位置关系,并证明你的猜想;
(2)试判断四边形BOCD的形状,并证明你的判断;
(3)已知AC=6,求扇形OBC所围成的圆锥的底面圆的半径r.
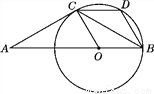
查看答案和解析>>
科目: 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:解答题
一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
(1)y与x的函数关系式为y=-x+150;(2)该批发商若想获得4000元的利润,应将售价定为70元;(3)该产品每千克售价为85元时,批发商获得的利润w(元)最大,此时的最大利润为4225元. 【解析】试题分析:(1)根据图表中的各数可得出y与x成一次函数关系,从而结合图表的数可得出y与x的关系式. (2)根据想获得4000元的利润,列出方程求解即可; (3)根据批发商获得的...查看答案和解析>>
科目: 来源:广东省东莞市翰林学校2017-2018学年八年级(上)期中数学试卷(word版含答案解析) 题型:单选题
点A(﹣3,2)关于y轴对称的点的坐标为( )
A. (3,﹣2) B. (3,2) C. (﹣3,﹣2) D. (2,﹣3)
B 【解析】【解析】 A(﹣3,2)关于y轴对称的点的坐标为(3,2).故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com