
科目: 来源:人教版八年级下册数学 第17章 勾股定理 单元检测卷 题型:填空题
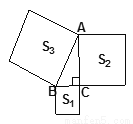
如图,以Rt△ABC的三边向外作正方形,其面积分别为S1,S2,S3,且S1=4,S2=8,则S3= .
查看答案和解析>>
科目: 来源:人教版八年级下册数学 第17章 勾股定理 单元检测卷 题型:解答题
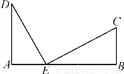
如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少千米处?
查看答案和解析>>
科目: 来源:人教版八年级下册数学 第17章 勾股定理 单元检测卷 题型:解答题
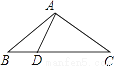
如图,△ABC中,AB=AC=20,BC=32,D是BC上一点,AD=15,且AD⊥AC,求BD长.
查看答案和解析>>
科目: 来源:人教版八年级下册数学 第17章 勾股定理 单元检测卷 题型:解答题
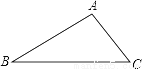
已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=2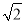 ,
,
求:(1)AB的长为________;
(2)S△ABC=________.
查看答案和解析>>
科目: 来源:人教版八年级下册数学 第17章 勾股定理 单元检测卷 题型:解答题
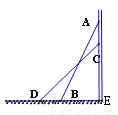
如图,将长为2.5米长的梯子AB斜靠在墙上,BE长0.7米。
(1)求梯子上端到墙的底端E的距离(即AE的长);
(2)如果梯子的顶端A沿墙下滑0.4米(即AC=0.4米),则梯脚B将外移(即BD长)多少米?
查看答案和解析>>
科目: 来源:2017-2018学年度人教版九年级数学下册第27 章同步课时练习:27.2.1 相似三角形的判定(第1课时) 题型:单选题
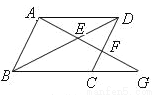
如图,在  ABCD中, G是 BC延长线上的一点, AG与 BD交于点 E,与 DC交与点 F,则图中相似三角形共有( )
ABCD中, G是 BC延长线上的一点, AG与 BD交于点 E,与 DC交与点 F,则图中相似三角形共有( )
A. 3对 B. 4对 C. 5对 D. 6对
D 【解析】∵四边形ABCD是平行四边形, ∴AB∥CD,AD∥BC, ∴△ABD∽△CDB,△GFC∽△GAB,△DEF∽△BEA,△AED∽△GEB,△ADF∽△GCF,△ADF∽△GBA. 即图中有6对相似三角形. 故选D.查看答案和解析>>
科目: 来源:2017-2018学年度人教版九年级数学下册第27 章同步课时练习:27.2.1 相似三角形的判定(第1课时) 题型:单选题
在梯形 ABCD中, AD∥BC,AC 、 BD交于 O,过点 O作 EF∥ AD,则图中相似三角形共有( )
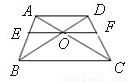
A. 3对 B. 4对 C. 5对 D. 6对
C 【解析】∵AD∥BC,EF∥AD,点O在EF上, ∴AD∥BC∥OE,AD∥BC∥OF, ∴△AOD∽△COB,△AOE∽△ACB,△DOF∽△DBC,△BEO∽△BAD,△COF∽△CAD. 即图中共有5对相似三角形. 故选C.查看答案和解析>>
科目: 来源:2017-2018学年度人教版九年级数学下册第27 章同步课时练习:27.2.1 相似三角形的判定(第1课时) 题型:单选题
如图,在△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边上的点F处,并且FD∥BC,则CD的长是( )
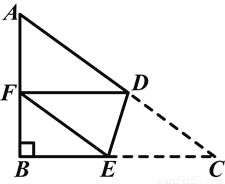
A. 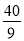
B. 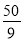
C. 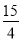
D. 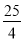
查看答案和解析>>
科目: 来源:2017-2018学年度人教版九年级数学下册第27 章同步课时练习:27.2.1 相似三角形的判定(第1课时) 题型:单选题
如图,在△ ABC中, DE∥ BC, DE分别与 AB 、 AC相交于点 D 、 E,若 AD=4, DB=2,则 DE∶ BC的值为( )
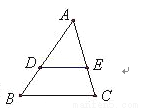
A. 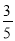 B.
B. 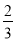 C.
C. 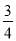 D.
D. 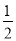
查看答案和解析>>
科目: 来源:2017-2018学年度人教版九年级数学下册第27 章同步课时练习:27.2.1 相似三角形的判定(第1课时) 题型:填空题
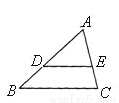
如图, DE与△ ABC的边 AB, AC分别相交于 D, E两点,且 DE∥ BC.若 DE=2cm, BC=3cm, EC=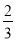 cm,则 AC=________cm.
cm,则 AC=________cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com