
科目: 来源:2017-2018学年八年级数学人教版上册 第14章 整式的乘法与因式分解 单元测试 题型:解答题
先化简,再求值:
(1)(9x3y-12xy3+3xy2)÷(-3xy)-(2y+x)(2y-x),其中x=1,y=-2;
(2)(m-n)(m+n)+(m+n)2-2m2,其中m、n满足方程组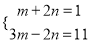
查看答案和解析>>
科目: 来源:2017-2018学年八年级数学人教版上册 第14章 整式的乘法与因式分解 单元测试 题型:解答题
(9分)(1)已知a-b=1,ab=-2,求(a+1)(b-1)的值;
(2)已知(a+b)2=11,(a-b)2=7,求ab;
(3)已知x-y=2,y-z=2,x+z=4,求x2-z2的值.
(1)-4;(2)1;(3)16 【解析】 (1)∵a-b=1,ab=-2, ∴原式=ab-(a-b)-1=-2-1-1=-4. (2)∵(a+b)2=a2+2ab+b2=11①,(a-b)2=a2-2ab+b2=7②, ①-②得4ab=4,∴ab=1. (3)由x-y=2,y-z=2,得x-z=4. 又∵x+z=4,∴原式=(x+z)(x-z)=16. ...查看答案和解析>>
科目: 来源:2017-2018学年八年级数学人教版上册 第14章 整式的乘法与因式分解 单元测试 题型:解答题
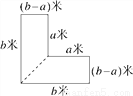
小红家有一块L形菜地,要把L形菜地按如图所示分成面积相等的两个梯形种上不同的蔬菜.已知这两个梯形的上底都是a米,下底都是b米,高都是(b-a)米.
(1)请你算一算,小红家的菜地面积共有多少平方米?
(2)当a=10,b=30时,面积是多少平方米?
查看答案和解析>>
科目: 来源:2017-2018学年八年级数学人教版上册 第14章 整式的乘法与因式分解 单元测试 题型:解答题
(10分)先阅读下列材料,再解答下列问题:
材料:因式分【解析】
(x+y)2+2(x+y)+1.
【解析】
将“x+y”看成整体,令x+y=A,则
原式=A2+2A+1=(A+1)2.
再将“A”还原,得原式=(x+y+1)2.
上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你解答下列问题:
(1)因式分【解析】
1+2(x-y)+(x-y)2=_______________;
(2)因式分【解析】
(a+b)(a+b-4)+4;
(3)求证:若n为正整数,则式子(n+1)(n+2)(n2+3n)+1的值一定是某一个整数的平方.
(1)(x-y+1)2;(2)见解析;(3)见解析. 【解析】分析:(1)把(x-y)看作一个整体,直接利用完全平方公式因式分解即可;(2)令A=a+b,带入后因式分解即可将原式因式分解;(3)将原式转化为(n²+3n) [(n+1)(n+2)]+1,进一步整理为(n²+3n+1) ²,根据n为正整数,从而说明原式是整数的平方. 本题解析: (1).1+2(x-y)+(x+y) ...查看答案和解析>>
科目: 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.2 实际问题与反比例函数(第1课时) 题型:填空题
京沈高速公路全长658km,汽车沿京沈高速公路从沈阳驶往北京,则汽车行完全程所需时间 t(h)与行驶的平均速度 v(km/h)之间的函数关系式为 .
t= 【解析】试题解析:由题意得: 汽车行驶完全程所需的时间t与行驶的平均速度v之间的函数关系式是t=. 故本题答案为:t=.查看答案和解析>>
科目: 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.2 实际问题与反比例函数(第1课时) 题型:填空题
完成某项任务可获得500元报酬,考虑由 x人完成这项任务,试写出人均报酬 y(元)与人数 x(人)之间的函数关系式 .
y= 【解析】试题解析:∵由x人完成报酬共为500元的某项任务, ∴xy=500, 即:y=. 故答案为:y=.查看答案和解析>>
科目: 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.2 实际问题与反比例函数(第1课时) 题型:填空题
近视眼镜的度数y(度)与镜片焦距x(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数y与镜片焦距x之间的函数关系式为 .
【解析】 试题分析:设反比例函数解析式为:y=,将x=0.25,y=400代入可得:k=100,则反比例函数的关系式为:y=.查看答案和解析>>
科目: 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.2 实际问题与反比例函数(第1课时) 题型:解答题
一定质量的氧气,它的密度  (kg/m 3)是它的体积 V(m 3)的反比例函数,当 V=10时,
(kg/m 3)是它的体积 V(m 3)的反比例函数,当 V=10时,  =1.43,
=1.43,
(1)求  与 V的函数关系式;
与 V的函数关系式;
(2)求当 V=2时氧气的密度  .
.
查看答案和解析>>
科目: 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.2 实际问题与反比例函数(第1课时) 题型:解答题
已知某矩形的面积为20cm 2.
(1)写出其长 y与宽 x之间的函数表达式.
(2)当矩形的长为12cm时,求宽为多少?当矩形的宽为4cm,求其长为多少?
(3)如果要求矩形的长不小于8cm,其宽至多要多少?
(1) y=( x>0);(2)当矩形的长为12cm时,宽为 cm;当矩形的宽为4cm时,其长为5cm;(3)宽至多是 cm. 【解析】试题分析:(1)利用矩形的面积公式列出两个变量之间的函数关系即可; (2)根据矩形的面积公式进行计算即可; (3)根据其增减性确定宽的取值范围即可. 试题解析:(1)∵xy=20, ∴y=( x>0); (2)∵面积为20cm ...查看答案和解析>>
科目: 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.2 实际问题与反比例函数(第1课时) 题型:解答题
小林家离工作单位的距离为3600米,他每天骑自行车上班时的速度为 v(米/分),所需时间为 t(分),
(1)则速度 v与时间 t之间有怎样的函数关系?
(2)若小林到单位用15分钟,那么他骑车的平均速度是多少?
(2)如果小林骑车的速度最快为300米/分,那他至少需要几分钟到达单位?
(1) ( t>0);(2) v=240;(3) t=12 【解析】试题分析:(1)根据速度、时间、路程的关系即可写出函数的关系式; (2)把t=15代入函数的解析式,即可求得速度; (3)把v=300代入函数解析式,即可求得时间. 试题解析:(1)反比例函数v=; (2)把t=15代入函数的解析式,得:v==240, 答:他骑车的平均速度是:240米/分; ...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com