
科目: 来源:人教版七年级下册 第1-3章 综合测试卷 题型:解答题
画一条数轴,在数轴上表示﹣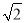 , 2,0,﹣
, 2,0,﹣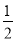 及它们的相反数,并比较所有数的大小,按从小到大的顺序用“<”连接起来.
及它们的相反数,并比较所有数的大小,按从小到大的顺序用“<”连接起来.
查看答案和解析>>
科目: 来源:人教版七年级下册 第1-3章 综合测试卷 题型:解答题
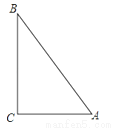
如图,点A表示小雨家,点B表示小樱家,点C表示小丽家,她们三家恰好组成一个直角三角形,其中AC⊥BC,AC=900米,BC=1200米,AB=1500米.
(1)试说出小雨家到街道BC的距离以及小樱家到街道AC的距离.
(2)画出表示小丽家到街道AB距离的线段.
查看答案和解析>>
科目: 来源:人教版七年级下册 第1-3章 综合测试卷 题型:解答题
如图,AB∥CD,∠B=78°,∠D=32°,求∠F的度数.
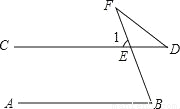
查看答案和解析>>
科目: 来源:人教版七年级下册 第1-3章 综合测试卷 题型:解答题
如图,已知∠1+∠2=180°,∠B=∠3,你能判断∠C与∠AED的大小关系吗?并说明理由.
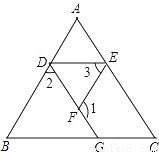
查看答案和解析>>
科目: 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
如图,已知AD//BE,∠1=∠2.求证:∠A=∠E.
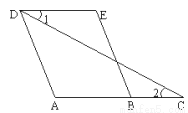
查看答案和解析>>
科目: 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
如图,DB∥FG∥EC,∠ABD=60°,∠ACE=36°,AP平分∠BAC.求∠PAG的度数.
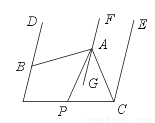
查看答案和解析>>
科目: 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
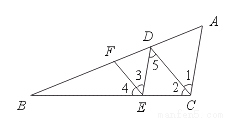
如图,已知AC∥DE,DC∥EF,CD平分∠BCD.求证:EF平分∠BED.
查看答案和解析>>
科目: 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
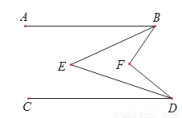
如图,AB∥CD,BE,DE分别平分∠ABF,∠FDC,试问∠E与∠F之间的数量关系如何?请说明理由.
查看答案和解析>>
科目: 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
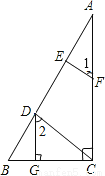
如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB
查看答案和解析>>
科目: 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
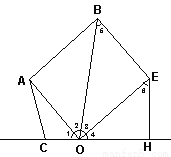
如图,BE∥AO,∠1=∠2,OE⊥OA于点O,EH⊥CO于点H,那么∠5=∠6,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com