
科目: 来源:北师大版九年级下册数学全册综合测试卷一 题型:填空题
一个扇形的面积为6πcm2,弧长为πcm,则该扇形的半径为 .
12cm. 【解析】 试题解析:设半径是r, ∵一个扇形的弧长是πcm,扇形的面积为6πcm2, ∴6π=×π×r, ∴r=12.查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷一 题型:填空题
在平面直角坐标系中,将函数y=﹣2x2的图象先向右平移1个单位长度,再向上平移5个单位长度,所得图象的函数表达式是 .
y=2(x﹣1)2+5. 【解析】试题分析:由“左加右减”的原则可知,抛物线y=﹣2x2的图象向右平移1个单位所得函数图象的关系式是:y=﹣2(x﹣1)2; 由“上加下减”的原则可知,抛物线y=﹣2(x﹣1)2的图象向上平移5个单位长度所得函数图象的关系式是:y=2(x﹣1)2+5.查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷一 题型:填空题
如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为 .
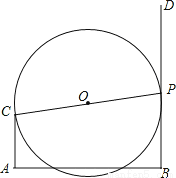
查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷一 题型:填空题
已知函数y=(k﹣3)x2+2x+1的图象与x轴有交点,则k的取值范围为 .
k≤4. 【解析】试题解析:∵二次函数y=(k﹣2)x2+2x+1的图象与x轴有交点, ∴一元二次方程(k﹣2)x2+2x+1=0有解, ∴, 解得:k≤3且k≠2. 故答案为:k≤3且k≠2.查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷一 题型:填空题
某服装店购进单价为15元的童装若干件,销售一段时间后发现:当销售价为25元时平均每天能售出8件,而当销售价每降低1元,平均每天能多售出2件.当每件的定价为_______元时,该服装店平均每天的销售利润最大.
22 【解析】试题分析:设定价为x元时,利润为w元,由题意建立w与x的二次函数关系:w=(x-15)(×4+8),化简得:w=,∵-2<0,∴当x===22时,w有最大值,∴当每件的定价为22元时,该服装店平均每天的销售利润最大.查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷一 题型:填空题
△OAB是以正多边形相邻的两个顶点A,B与它的中心O为顶点的三角形,若△OAB的一个内角为70°,则该正多边形的边数为_____.
9 【解析】分两种情况讨论:若∠OAB=∠OBA=70°,则∠BOA=40°,边数为: =9; 若∠BOA=70°,则边数为: 不为整数,故不存在。综上所述,边数为9。查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷一 题型:解答题
如图,⊙O的直径AB垂直弦CD于点E,点F在AB的延长线上,且∠BCF=∠A.
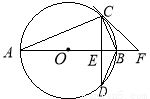
(1)求证:直线CF是⊙O的切线;
(2)若⊙O的半径为5,DB=4.求sin∠D的值.
(1)证明见解析;(2). 【解析】 试题分析:(1)连接OC,由OA=OA可知∠ACO=∠A,再根据∠FCB=∠A可知∠ACO=∠FCB,由于AB是⊙O的直径,所以∠ACO+∠OCB=90°故∠FCB+∠OCB=90°故可得出结论; (2)由AB是⊙O的直径,CD⊥AB可知 试题解析: (1)连接OC, ∵OA=OC, ∴∠ACO=∠A, 又∵∠FCB=...查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷一 题型:解答题
如图,AB是⊙O的直径,AC是弦,半径OD⊥AC于点E,过点D的切线与BA延长线交于点F.
(1)求证:∠CDB=∠BFD;
(2)若AB=10,AC=8,求DF的长.
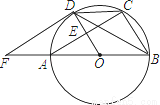
查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷一 题型:解答题
水利部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD,如图所示,已知迎水坡面AB的长为16米,∠B=60°,背水坡面CD的长为16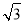 米,加固后大坝的横截面为梯形ABED,CE的长为8米.
米,加固后大坝的横截面为梯形ABED,CE的长为8米.
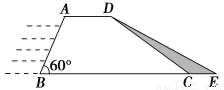
(1)已知需加固的大坝长为150米,求需要填土石方多少立方米?
(2)求加固后的大坝背水坡面DE的坡度.
(1)需填土4 800 (立方米);(2)DE的坡度为. 【解析】 【解析】 分别作AF⊥BC,DG⊥BC,垂点分别为F、G, 如图所示 在Rt△ABF中,AB=16米,∠B=60°, sin ∠B=, ∴AF=16×=8, DG=8, ∴S△DCE=×CE×DG=×8×8=32, 需要填土:150×32=4 800 (立方米) (2)...查看答案和解析>>
科目: 来源:北师大版九年级下册数学全册综合测试卷一 题型:解答题
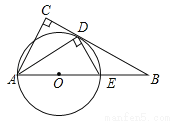
如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径.
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB=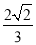 ,AE=4,求CD.
,AE=4,求CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com