练习册

  • 练习册
  • 试题
    相关习题
     0  321924  321932  321938  321942  321948  321950  321954  321960  321962  321968  321974  321978  321980  321984  321990  321992  321998  322002  322004  322008  322010  322014  322016  322018  322019  322020  322022  322023  322024  322026  322028  322032  322034  322038  322040  322044  322050  322052  322058  322062  322064  322068  322074  322080  322082  322088  322092  322094  322100  322104  322110  322118  366461 

    科目： 来源：2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型：单选题

    八年级1班生活委员小华去为班级购买两种单价分别为8元和10元的盆栽，共有100元，若小华将100元恰好用完，共有几种购买方案（ ）

    A. 2 B. 3 C. 4 D. 5

    A 【解析】【解析】 设购买单价为8元的盆栽x盆，购买单价为10元的盆栽y盆，根据题意可得： 8x+10y=100，当x=10，y=2，当x=5，y=6，当x=0，y=10（不合题意，舍去）． 故符合题意的有2种，故选A．

    查看答案和解析>>

    科目： 来源：2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型：单选题

    如图，正方形ABCD的边长为2，动点P从C出发，在正方形的边上沿着C→B→A的方向运动(点P与A不重合)．设P的运动路程为x，则下列图象表示△ADP的面积y关于x的函数关系的是(　　)

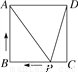
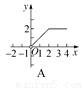
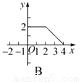
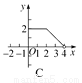
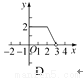
    C 【解析】【解析】 当P点由C运动到B点时，即0≤x≤2时，y=×2×2=2； 当P点由B运动到A点时（点P与A不重合），即2＜x＜4时，y=×2×（4-x）=4﹣x ∴y关于x的函数关系： 注：图象不包含x=4这个点． 故选C．

    查看答案和解析>>

    科目： 来源：2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型：单选题

    如图，把长方形纸片ABCD折叠，使其对角顶点C与A重合．若长方形的长BC为8，宽AB为4，则折痕EF的长度为(　　)

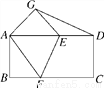
    A. 5 B. 3 C. 2 D. 3

    C 【解析】过F点作FH⊥AD于H，在Rt△EHF中根据勾股定理即可求出EF的长． 【解析】 如图所示，过F点作FH⊥AD于H， 设CF=x，则BF=8?x， 在Rt△ABF中,AB2+BF2=AF2， ∴16+(8?x)2=x2， 解得：x=5， ∴AF=CF=5， ∵AD//BC, ∴∠AEF-∠EFC, 又∵∠AFE-∠EFC, ...

    查看答案和解析>>

    科目： 来源：2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型：单选题

    直角三角形的两条直角边长分别是3，4，则该直角三角形的斜边长是(　　)

    A. 2 B. 3 C. 4 D. 5

    D 【解析】根据勾股定理即可得出答案. 【解析】 ∵直角三角形的两条直角边长分别是3，4， ∴该直角三角形的斜边长是： 故选D.

    查看答案和解析>>

    科目： 来源：2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型：单选题

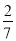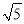    在实数－，0，π， ，1.41中，无理数有(　　)

    A. 4个 B. 3个 C. 2个 D. 1个

    C 【解析】根据无理数的定义：无限不循环小数是无理数，对各数分别判断即可. 【解析】 在实数－，0，π， ，1.41中，无理数有π和，共2个. 故选C.

    查看答案和解析>>

    科目： 来源：2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型：单选题

    如图，下列条件不能判断直线a∥b的是（ ）

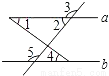
    A. ∠1=∠4 B. ∠3=∠5 C. ∠2+∠5=180° D. ∠2+∠4=180°

    D 【解析】试题解析：A、能判断，∵∠1=∠4，∴a∥b，满足内错角相等，两直线平行． B、能判断，∵∠3=∠5，∴a∥b，满足同位角相等，两直线平行． C、能判断，∵∠2+∠5=180°，∴a∥b，满足同旁内角互补，两直线平行． D、不能． 故选D．

    查看答案和解析>>

    科目： 来源：2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型：单选题

    在某校冬季运动会上，有15名选手参加了200米预赛，取前八名进入决赛．已知参赛选手成绩各不相同，某选手要想知道自己是否进入决赛，除了知道自己的成绩外，还需要了解全部成绩的(　　)

    A. 平均数 B. 中位数 C. 众数 D. 方差

    B 【解析】一组数据从小到大（或从大到小）排列，中位数最中间一个数据或两个数据的平均数；15人成绩的中位数是第8名的成绩．参赛选手要想知道自己是否能进入前8名，只需要了解自己的成绩以及全部成绩的中位数，比较即可． 【解析】 由于总共有15个人，且他们的分数互不相同，第8的成绩是中位数，所以要判断是否进入前8名，只需要了解自己的成绩以及全部成绩的中位数. 故选B.

    查看答案和解析>>

    科目： 来源：2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型：单选题

    如图所示，若点E的坐标为(－2，1)，点F的坐标为(1，－1)，则点G的坐标为(　　)

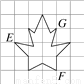
    A. (1，2) B. (2，2) C. (2，1) D. (1，1)

    A 【解析】根据点E，F的坐标分别确定出坐标轴及原点的位置并建立平面直角坐标系，即可得出点G的坐标． 【解析】 由点E坐标为(?2,1),点F坐标为(1,?1)可知左数第四条竖线是y轴,点E与点F中间的横线是x轴,其交点是原点,则点G的坐标为(1,2). 故选A.

    查看答案和解析>>

    科目： 来源：2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型：填空题

    化简： =

    3。 【解析】.

    查看答案和解析>>

    科目： 来源：2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型：填空题

    如图，AB∥CD，EF与AB，CD分别相交于点E，F，EP⊥EF，与∠EFD的平分线FP相交于点P.若∠BEP＝46°，则∠EPF＝________°.

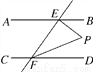
    68 【解析】由AB∥CD，根据两直线平行，同旁内角互补，即可得∠BEF+∠DFE=180°，又由EP⊥EF，∠EFD的平分线与EP相交于点P，∠BEP=46°，即可求得∠PFE的度数，然后根据三角形的内角和定理，即可求得∠EPF的度数． 【解析】 ∵AB∥CD， ∴∠BEF+∠DFE=180°， ∴EP⊥EF， ∴∠PEF=90°， ∵∠BEP=36°， ...

    查看答案和解析>>

    同步练习册答案