
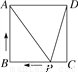
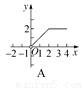
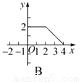
��ͼ��������ABCD�ı߳�Ϊ2������P��C�������������εı�������C��B��A�ķ����˶�(��P��A���غ�)����P���˶�·��Ϊx��������ͼ���ʾ��ADP�����y����x�ĺ�����ϵ����(����)
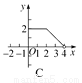
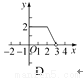

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ�����м��� ���ͣ������
��ͼ���ڡ�ABC�У�D��E�ֱ��DZ�AB��AC�ϵĵ㣬��DE��BC������ADE���ABC���ܳ�֮��Ϊ2��3��AD��4����DB��_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ�²����� ������ ����֮��Ĺ�ϵ ���ͣ������
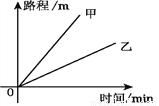
��ͼ�Ǽס��������˶�Ա�����г�����������·����ʱ��Ĺ�ϵͼ��,����ٶ�____________�ҵ��ٶ�(�á�>����=����<�����).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ��ʦ����ϲ� ȫ���ۺϲ��Ծ� ���ͣ������
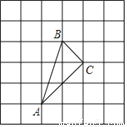
��ͼ��С�����εı߳�Ϊ1����ABC���������㶼��С�����εĶ��㴦���жϡ�ABC����״���������ABC�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ��ʦ����ϲ� ȫ���ۺϲ��Ծ� ���ͣ���ѡ��
��ijУ�����˶����ϣ���15��ѡ�ֲμ���200��Ԥ����ȡǰ���������������֪����ѡ�ֳɼ�������ͬ��ijѡ��Ҫ��֪���Լ��Ƿ�������������֪���Լ��ijɼ��⣬����Ҫ�˽�ȫ���ɼ���(����)
A. ƽ���� B. ��λ�� C. ���� D. ����
B ��������һ�����ݴ�С����Ӵ�С�����У���λ�����м�һ�����ݻ��������ݵ�ƽ������15�˳ɼ�����λ���ǵ�8���ijɼ�������ѡ��Ҫ��֪���Լ��Ƿ��ܽ���ǰ8����ֻ��Ҫ�˽��Լ��ijɼ��Լ�ȫ���ɼ�����λ�����Ƚϼ��ɣ� �������� �����ܹ���15���ˣ������ǵķ���������ͬ����8�ijɼ�����λ��������Ҫ�ж��Ƿ����ǰ8����ֻ��Ҫ�˽��Լ��ijɼ��Լ�ȫ���ɼ�����λ��. ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ�²�4.2ͼ�ε�ȫ����ϰ ���ͣ������
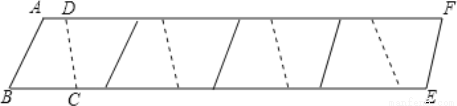
��ͼ��ʾ��ͼ������ȫ�ȵ�ͼ��ƴ�ɵģ�����AD=0.5cm��BC=1cm����AF�ij���Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ�²�4.2ͼ�ε�ȫ����ϰ ���ͣ���ѡ��
��֪ͼ�е�����������ȫ�ȣ���Ϧ��Ķ����ǣ�������
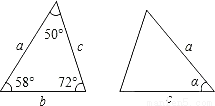
A. 72�� B. 60�� C. 58�� D. 50��
D �������� ��ͼ��ɵã���ABC�ա�DEF, ���A=��D=50�㣬��C=��F=72�㣬 ���1=180�㣭50�㣭72��=58��. ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰����꼶��ѧ�²���ϰ�������´����� ���ͣ���ѡ��
��ͼ��ֱ��AB��CD�ཻ�ڵ�O������OMƽ�֡�AOC��ON��OM������AOM=35�㣬���CON�Ķ���Ϊ�� ��
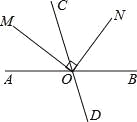
A. 35�� B. 45�� C. 55�� D. 65��
C ����������ΪON��OM,��CON=55��,���ԡ�COM=90�㣭��CON=90�㣭55��=35��, ����ΪOMƽ�֡�AOC,���ԡ�AOC=��COM=35��,��ѡA.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ�²�ͬ��Ҫ��3.2 �ù�ϵʽ��ʾ�ı������ϵ ���ͣ���ѡ��
һ��Ϊ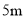 ����Ϊ
����Ϊ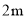 �ij�����ľ�壬��Ҫ�ڳ����Ͻ�ȥ��Ϊ
�ij�����ľ�壬��Ҫ�ڳ����Ͻ�ȥ��Ϊ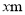 ��һ���֣���ͼ������ʣ��ľ������
��һ���֣���ͼ������ʣ��ľ������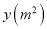 ��
��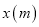 �Ĺ�ϵʽΪ������
�Ĺ�ϵʽΪ������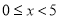 ���� ����
���� ����

A. 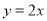 B.
B. 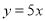 C.
C. 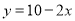 D.
D. 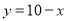
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com