(4 xm-5 y2) (4 xm+5y2)＝_______．

16 x2m-25 y4 【解析】根据平方差公式可得原式=.

(x+y-z) (x-y-z)＝（__________） 2-（__________） 2．

x-z y 【解析】(x+y-z) (x-y-z)＝.

若x2-y2=48，x+y=6，则3x-3y=_____．

24 【解析】∵x2-y2=（x+y）（x-y）=48，x+y=6， ∴x-y=8， ∴3x-3y=3（x-y）=24.

(x-_____-3)(x+2y-_____)=[________-2y][ ________+2y]

2y 3 x-3 x-3 【解析】观察所给的算式，根据平方差公式的特点可得： ，所以答案为2y 、 3 、 x-3 、x-3.

观察下列各式：(a-1)(a+1)=a2-1，(a-1)(a2+a+1)=a3-1，(a-1)(a3+a2+a+1)=a4-1…根据前面各式的规律计算：(a-1)(a4+a3+a2+a+1)=_____；22012+22011+…+22+2+1=_____．

a5-1 22013-1 【解析】观察题目中所给的算式可得(a-1)(a4+a3+a2+a+1)= a5-1； 22012+22011+…+22+2+1 =（2-1）（22012+22011+…+22+2+1） =2×（22012+22011+…+22+2+1）-（22012+22011+…+22+2+1） =22013+22012+22011+…+22+2-2201...

计算: ( a－2b ) ( －2b－a ) ．

-a2+4b2 【解析】试题分析：根据平方差公式直接计算即可. 试题解析： 原式=.

若x2+y2=86，xy=-16，求(x-y)2．

118 【解析】试题分析：根据完全平方公式得到（x-y）2=x2+y2-2xy，然后把x2+y2=86，xy=-16代入计算即可． 试题解析： ∵（x-y）2=x2+y2-2xy，且x2+y2=86，xy=-16， ∴（x-y）2=86-2×（-16）=118．

已知：x2+xy+y=14，y2+xy+x=28，求x+y的值．

-7或6 【解析】试题分析：由x2+xy+y=14，y2+xy+x=28，即可求得x2+2xy+y2+x+y=42，则变形得（x+y）2+（x+y）-42=0，将x+y看作整体，利用因式分解法即可求得x+y的值． 试题解析： ∵x2+xy+y=14①，y2+xy+x=28②， ∴①+②，得：x2+2xy+y2+x+y=42， ∴（x+y）2+（x+y）-42=0， ...

先化简，再求值：（a2b-2ab2-b3）÷b-（a+b）（a-b），其中a=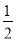，b= -1.

-2ab，1 【解析】试题分析：先乘除，然后合并同类项，代入求值即可. 试题解析：原式 将代入上式得：原式

如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘 数”．如：4＝22-02，12＝42-22，20＝62-42，因此4，12，20这三个数都是神秘数．

(1)28和2012这两个数是神秘数吗?为什么?

(2)设两个连续偶数为2k+2和2k(其中k取非负整数)，由这两个连续偶数构造的神秘数是4的倍数吗?为什么?

(3)两个连续奇数的平方差(取正数)是神秘数吗?为什么?

(1)28和2012都是神秘数 (2)这两个连续偶数构造的神秘数是4的倍数(3)两个连续奇数的平方差不是神秘数． 【解析】试题分析： （1）将神秘数4开始，将一些神秘数写成如下的形式4=2×2＝22-02，12＝2×6＝42-22，20＝2×10＝62-42，…，则可判断28和2012这两个数是不是神秘数； （2）将这两个数平方相减，判断它们的差是不是4的倍数； （3）用n...