
(x+y-z) (x-y-z)=(__________) 2-(__________) 2.
x-z y 【解析】(x+y-z) (x-y-z)=.科目:初中数学 来源:北师大版七年级数学下3.3 用图象表示的变量间关系 同步练习 题型:单选题
小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离y(米)与时间t(分钟)之间关系的大致图象是( )
A. 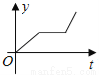 B.
B. 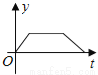 C.
C. 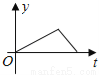 D.
D. 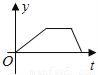
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.1.1 三角形及其内角和 同步练习 题型:单选题
如图,在△ABC中,点D、E、F分别是三条边上的点,EF∥AC,DF∥AB,∠B=45°,∠C=60°.则∠EFD=( )
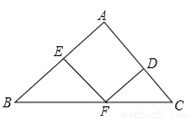
A. 80° B. 75° C. 70° D. 65°
B 【解析】试题分析:根据EF∥AC,求出∠EFB=∠C=60°,再根据DF∥AB,求出∠DFC=∠B=45°,从而求出∠EFD=180°﹣60°﹣45°=75°. 故选B查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.3.1 用“边边边”判定三角形全等 同步练习 题型:单选题
如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:
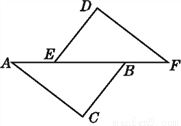
①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A. ①或② B. ②或③ C. ①或③ D. ①或④
A 【解析】由题意可得,要用SSS进行△ABC和△FED全等的判定,需要AB=FE, 若添加①AE=FB,则可得AE+BE=FB+BE,即AB=FE, 故①可以; 若添加AB=FE,则可直接证明两三角形的全等,故②可以。 若添加AE=BE,或BF=BE,均不能得出AB=FE,不可以利用SSS进行全等的证明,故③④不可以。 故选A.查看答案和解析>>
科目:初中数学 来源:2017年北师大七年级下1.5《平方差公式》练习题 题型:解答题
若x2+y2=86,xy=-16,求(x-y)2.
118 【解析】试题分析:根据完全平方公式得到(x-y)2=x2+y2-2xy,然后把x2+y2=86,xy=-16代入计算即可. 试题解析: ∵(x-y)2=x2+y2-2xy,且x2+y2=86,xy=-16, ∴(x-y)2=86-2×(-16)=118.查看答案和解析>>
科目:初中数学 来源:2017年北师大七年级下1.5《平方差公式》练习题 题型:单选题
计算:a2-(a+1)(a-1)的结果是( )
A. 1 B. -1 C. 2a2+1 D. 2a2-1
A 【解析】原式=,故选A.查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册4.3.2探索三角形全等的条件练习 题型:解答题
如图,已知,在四边形ABCD中,E是AC上一点,∠DAC=∠BAC,∠DCA=∠BCA.求证:∠DEC=∠BEC。
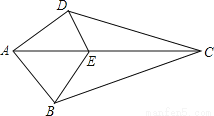
查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第三章3.1用表格表示的变量间关系课时练习 题型:填空题
水中涟漪(圆形水波)不断扩大,记它的半径为r,圆周长为C,圆周率(圆周长与直径的比)为π,指出其中的变量为______.
圆的半径r和圆的周长C 【解析】根据函数的定义:函数中的每个值x,变量y按照一定的法则有一个确定的值y与之对应,可知自变量是圆的半径r,因变量是圆的周长C. 故答案为:圆的半径r和圆的周长C.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型:单选题
已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为( )
A. 2cm B. 3cm C. 4cm D. 5cm
B 【解析】试题解析:设大小处于中间的边长是xcm,则最大的边是(x+1)cm,最小的边长是(x?1)cm. 则(x+1)+x+(x?1)=12, 解得:x=4, 则最短的边长是:4?1=3cm. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com