
科目: 来源:北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型:单选题
已知三角形的三边长分别为4,5,x,则x不可能是( )
A. 3 B. 5 C. 7 D. 9
D 【解析】试题解析:5-4<x<5+4,即1<x<9,则x的不可能的值是9, 故选D. 考点:1.三角形三边关系;2.解一元一次不等式组.查看答案和解析>>
科目: 来源:北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型:单选题
已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为( )
A. 2cm B. 3cm C. 4cm D. 5cm
B 【解析】试题解析:设大小处于中间的边长是xcm,则最大的边是(x+1)cm,最小的边长是(x?1)cm. 则(x+1)+x+(x?1)=12, 解得:x=4, 则最短的边长是:4?1=3cm. 故选B.查看答案和解析>>
科目: 来源:北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型:单选题
在等腰△ABC中,AB=AC,其周长为20cm,则AB边的取值范围是( )
A. 1cm<AB<4cm B. 5cm<AB<10cm
C. 4cm<AB<8cm D. 4cm<AB<10cm
B 【解析】试题分析:∵在等腰△ABC中,AB=AC,其周长为20cm,∴设AB="AC=x" cm,则BC=(20﹣2x)cm,∴,解得5cm<x<10cm.故选B.查看答案和解析>>
科目: 来源:北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型:单选题
一个等腰三角形的两边长分别是3和7,则它的周长为( )
A. 17 B. 15 C. 13 D. 13或17
A 【解析】试题分析:当3为腰时,则3+3=6<7,不能构成三角形,则等腰三角形的腰长为7,底为3,则周长为:7+7+3=17.查看答案和解析>>
科目: 来源:北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型:解答题
科目: 来源:北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型:解答题
把一条长为18米的细绳围成一个三角形,其中两边长分别为x米和4米.
(1)求x的取值范围;
(2)若围成的三角形是等腰三角形,求x的值.
(1)5(2)x=7. 【解析】试题分析: (1)由题意可知围成的三角形的周长为18米,结合其中两边长为x米和4米,可得第三边为(18-x-4)米,再根据三角形三边间的关系列出不等式组,即可求得x的取值范围; (2)分x为底边和腰两种情况分别列出方程,可解得对应的x的值,再由三角形三边间的关系检验是否符合题意即可求得x的值. 试题解析: (1)由题意可得:18-4-x...查看答案和解析>>
科目: 来源:北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型:解答题
如图,已知P是△ABC内部的一点.
(1)度量AB,AC,PB,PC的长,根据度量结果比较AB+AC与PB+PC的大小.
(2)改变点P的位置,上述结论还成立吗?请说明理由.
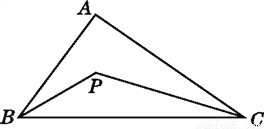
查看答案和解析>>
科目: 来源:北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型:解答题
在平面内,分别用3根、5根、6根……火柴棒首尾依次相接,能搭成什么形状的三角形呢?通过尝试,列表如下.
火柴棒数 | 3 | 5 | 6 | … |
示意图 |
|
|
| … |
形状 | 等边三角形 | 等腰三角形 | 等边三角形 | … |
问:(1)4根火柴棒能搭成三角形吗?
(2)8根、12根火柴棒分别能搭成几种不同形状的三角形?并画出它们的示意图.
(1)4根火柴棒不能搭成三角形(2)8根火柴棒能搭成一种三角形,12根火柴棒能搭成三种不同的三角形:(4,4,4),(5,5,2),(3,4,5) 【解析】试题分析: (1)由“三角形三边间的关系”可知,四根火柴棒不能围成三角形; (2)结合“三角形三边间的关系”分析可知:①8根火柴棒能搭成一种三角形,其边长分别为2、3、3,再根据边长画出示意图即可;②12根火柴棒可以搭成三种三...查看答案和解析>>
科目: 来源:北师大七年级下1.7 整式的除法 同步练习含答案 题型:单选题
计算–12a6÷3a2的结果是( )
A. –4a3 B. –4a8 C. –4a4 D. – a4
a4
查看答案和解析>>
科目: 来源:北师大七年级下1.7 整式的除法 同步练习含答案 题型:单选题
下列计算正确的是( )
A. x2+3x2=4x4 B. x2y·2x3=2x4y
C. (6x2y2)÷(3x)=2x2 D. (-3x)2=9x2
D 【解析】A. ∵ x2+3x2=4x2 ,故不正确; B. ∵x2y·2x3=2x5y,故不正确; C. ∵ (6x2y2)÷(3x)=2xy2,故不正确; D. ∵ (-3x)2=9x2,故正确; 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com