练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知三角形的三边长为连续整数，且周长为12cm，则它的最短边长为（　　）

    A. 2cm B. 3cm C. 4cm D. 5cm

    B 【解析】试题解析：设大小处于中间的边长是xcm，则最大的边是(x+1)cm，最小的边长是(x?1)cm. 则(x+1)+x+(x?1)=12， 解得：x=4， 则最短的边长是：4?1=3cm. 故选B.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年北师大七年级下1.5《平方差公式》练习题 题型：填空题

    (x+y-z) (x-y-z)＝（__________） 2-（__________） 2．

    x-z y 【解析】(x+y-z) (x-y-z)＝.

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第三章3.1用表格表示的变量间关系课时练习 题型：单选题

    下面的表格列出了一个实验的统计数据，表示将皮球从高处落下时，弹跳高度b与下降高度d的关系，下面能表示这种关系的式子是（　　）

    d

    50

    80

    100

    150

    b

    25

    40

    50

    75

    A. b=d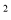 B. b=2d C. b= d D. b=d+25

    C 【解析】这是一个用图表表示的函数，可以看出d是b的2倍，即可得关系式． 【解析】 由统计数据可知： d是b的2倍， 所以，b=． 故本题选C．

    查看答案和解析>>

    科目：初中数学 来源：北师大七年级下1.7 整式的除法 同步练习含答案 题型：单选题

    已知a=1.6×109,b=4×103,则a2÷b等于(　　)

    A. 4×107 B. 8×1014

    C. 6.4×105 D. 6.4×1014

    D 【解析】根据题意得到a2÷b=（1.6×109）2÷（4×103），根据积的乘方得到原式=1.6×1.6×1018÷（4×103），再根据同底数的幂的除法法则得到原式=6.4×1014． 【解析】 a2÷b=（1.6×109）2÷（4×103）=1.6×1.6×1018÷（4×103）=6.4×1014． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型：解答题

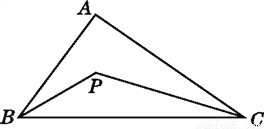
    如图,已知P是△ABC内部的一点.

    (1)度量AB,AC,PB,PC的长,根据度量结果比较AB+AC与PB+PC的大小.

    (2)改变点P的位置,上述结论还成立吗?请说明理由.

    (1)AB+AC>PB+PC(2)成立 【解析】试题分析： （1）使用刻度尺测量出四条线段的长度，再计算比较即可； （2）改变点P的位置，（1）中所得结论仍然成立，延长BP交AC于点D，利用三角形三边间的关系结合不等式的性质即可证明结论仍然成立. 试题解析： （1）度量结果略，可得结论：AB+AC>PB+PC； （2）在△ABC的内部改变点P的位置，（1）中所得...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型：单选题

    若一个三角形的两边长分别为3和7，则第三边长可能是（ ）

    A．6 B．3 C．2 D．11

    A. 【解析】 试题分析：根据三角形三边关系，两边之和第三边，两边之差小于第三边可得4＜第三边长＜10，所以符合条件的整数为6，故答案选A．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型：单选题

    一个等腰三角形的两边长分别为4，8，则它的周长为（　　）

    A. 12 B. 16 C. 20 D. 16或20

    C 【解析】试题分析：由于题中没有指明哪边是底哪边是腰，则应该分两种情况进行分析． ①当4为腰时，4+4=8，故此种情况不存在；②当8为腰时，8﹣4＜8＜8+4，符合题意． 故此三角形的周长=8+8+4=20．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型：填空题

    已知三角形的三条中线交于一点,则下列结论:①这一点在三角形的内部;②这一点有可能在三角形的外部;③这一点是三角形的重心.其中正确的结论有____.(填序号)

    ①③ 【解析】【解析】 三角形的三条中线的交点一定在三角形内部，这个交点叫三角形的重心．故①③正确．故答案为：①③．

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    在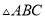中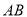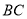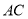， 、、三边的长分别为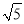、、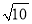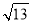，求这个三角形的面积．

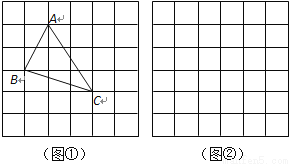
    小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点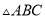（即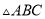三个顶点都在小正方形的顶点处），如图所示．这样不需求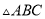的高，而借用网格就能计算出它的面积．

    （1）请你将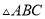的面积直接填写在横线上．__________________

    思维拓展：

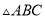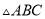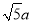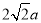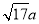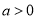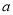    （2）我们把上述求面积的方法叫做构图法．若三边的长分别为、、（），请利用图的正方形网格（每个小正方形的边长为）画出相应的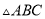，并求出它的面积．

    探索创新：

    （3）若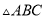三边的长分别为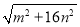、、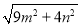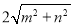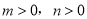（，且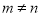），试运用构图法求出这三角形的面积．（请用2B铅笔将所作图形加黑加粗）

    （1）；（2）作图见解析； ；（3）作图见解析； . 【解析】利用恰好能覆盖△ABC的边长为的小正方形的面积减去三个小直角三角形的面积即可解答；

    查看答案和解析>>

    同步练习册答案