
科目: 来源:北师大版七年级下册4.3 探索三角形全等的条件(2)(ASA,AAS) 题型:解答题
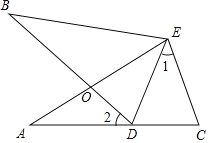
如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE,BD交于点O;
求证:△AEC≌△BED;
查看答案和解析>>
科目: 来源:北师大版七年级下册4.3 探索三角形全等的条件(2)(ASA,AAS) 题型:解答题
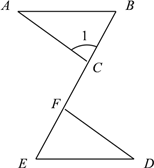
如图,已知点B、C、F、E在同一直线上,∠A=∠D,BF=EC,AB//DE ,若∠1=80°,求∠BFD的度数;
查看答案和解析>>
科目: 来源:北师大版七年级下册4.3 探索三角形全等的条件(2)(ASA,AAS) 题型:解答题
如图①,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.
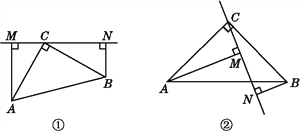
(1)试说明:MN=AM+BN.
(2)如图②,若过点C作直线MN与线段AB相交,AM⊥MN于点M,BN⊥MN于点N(AM>BN),(1)中的结论是否仍然成立?说明理由.
查看答案和解析>>
科目: 来源:人教版数学中考专题复习 阅读理解问题重点精讲课后练习 题型:解答题
阅读下面材料:
如图1,已知线段AB、CD相交于点O,且AB=CD,请你利用所学知识把线段AB、CD转移到同一三角形中。
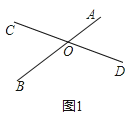
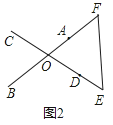
小强同学利用平移知识解决了此问题,具体做法如下:
如图2,延长OD至点E,使DE=CO,延长OA至点F,使AF=OB,连接EF,则△OEF为所求的三角形。
请你仔细体会小强的做法,探究并解答下列问题:
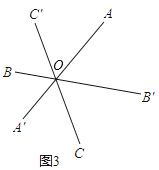
如图3,长为2的三条线段AA′,BB′,CC′交于一点O,并且∠B′OA=∠C′OB=∠A′OC=60°;
(1)请你把三条线段AA′,BB′,CC′ 转移到同一三角形中。(简要叙述画法)
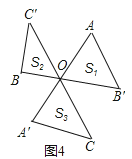
(2)连接AB′、BC′、CA′,如图4,设△AB′O、△BC′O、△CA′O的面积分别为S1、S2、S3,则S1+S2+S3________(填“>”或“<”或“=”)。
查看答案和解析>>
科目: 来源:人教版数学中考专题复习 阅读理解问题重点精讲课后练习 题型:解答题
已知点P是矩形ABCD边AB上的任意一点(与点A、B不重合)
(1)如图①,现将△PBC沿PC翻折得到△PEC;再在AD上取一点F,将△PAF沿PF翻折得到△PGF,并使得射线PE、PG重合,试问FG与CE的位置关系如何,请说明理由;
(2)在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的大小关系,并说明你的理由;
(3)如图③,分别在AD、BC上取点F、C’,使得∠APF=∠BPC’,与(1)中的操作相类似,即将△PAF沿PF翻折得到△PFG,并将△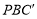 沿
沿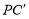 翻折得到△
翻折得到△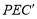 ,连接
,连接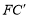 ,取
,取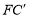 的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.
的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.

查看答案和解析>>
科目: 来源:人教版数学中考专题复习 阅读理解问题重点精讲课后练习 题型:解答题
我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积。用现代式子表示即为: 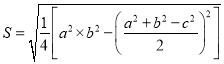 …①(其中a、b、c为三角形的三边长,S为面积)。
…①(其中a、b、c为三角形的三边长,S为面积)。
而另一个文明古国古希腊也有求三角形面积的海伦公式:
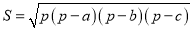 …②(其中
…②(其中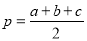 )。
)。
(1)若已知三角形的三边长分别为5,7,8,试分别运用公式①和公式②,计算该三角形的面积S;
(2)你能否由公式①推导出公式②?请试试。
查看答案和解析>>
科目: 来源:2018苏科版八年级数学下册 第10章《分式》综合提高卷 题型:单选题
用换元法解分式方程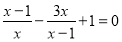 时,如果设
时,如果设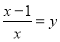 ,将原方程化为关于
,将原方程化为关于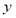 的整式方程,那么这个整式方程是( )
的整式方程,那么这个整式方程是( )
A.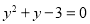 B.
B.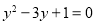 C.
C.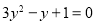 D.
D.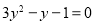
查看答案和解析>>
科目: 来源:2018苏科版八年级数学下册 第10章《分式》综合提高卷 题型:单选题
已知关于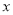 的分式方程
的分式方程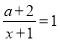 的解是非正数,则以的取值范围是 ( )
的解是非正数,则以的取值范围是 ( )
A. 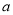 ≤一1 B.
≤一1 B. 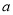 ≤一1且
≤一1且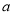 ≠一2
≠一2
C. 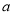 ≤1且
≤1且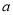 ≠2 D.
≠2 D. 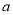 ≤1
≤1
查看答案和解析>>
科目: 来源:2018苏科版八年级数学下册 第10章《分式》综合提高卷 题型:单选题
甲车行驶30千米与乙车行驶40千米所用时间相同,已知乙车每小时比甲车多行驶15千米,设甲车的速度为x千米/小时,依据题意列方程正确的是( )
A.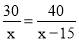 B.
B.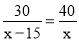 C.
C.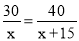 D.
D.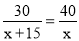
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com