
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:解答题
计算:( )﹣2﹣
)﹣2﹣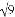 +(
+(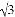 ﹣4)0﹣
﹣4)0﹣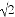 cos45°.
cos45°.
【答案】1
【解析】试题分析:把原式的第一项根据负整数指数幂的意义化简,第二项根据算术平方根的定义求出9的算术平方根,第三项根据零指数公式化简,最后一项利用特殊角的三角函数值化简,合并后即可求出值.
试题解析:原式=4﹣3+1﹣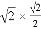
=2﹣1
=1.
【题型】解答题
【结束】
16
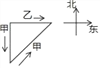
《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙行各几何”.大意是说,已知甲、乙二人同时从同一地
点出发,甲的速度为7,乙的速度为3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲、乙各走了多远?
查看答案和解析>>
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:解答题
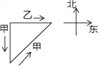
《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙行各几何”.大意是说,已知甲、乙二人同时从同一地
点出发,甲的速度为7,乙的速度为3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲、乙各走了多远?
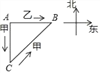
【答案】甲走了24.5步,乙走了10.5步
【解析】试题分析:设经x秒二人在B处相遇,然后利用勾股定理列出方程即可求得甲乙两人走的步数.
试题解析:设经x秒二人在B处相遇,这时乙共行AB=3x,
甲共行AC+BC=7x,
∵AC=10,
∴BC=7x﹣10,
又∵∠A=90°,
∴BC2=AC2+AB2,
∴(7x﹣10)2=102+(3x)2,
∴x=0(舍去)或x=3.5,
∴AB=3x=10.5,
AC+BC=7x=24.5,
答:甲走了24.5步,乙走了10.5步.
【题型】解答题
【结束】
17
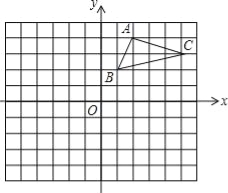
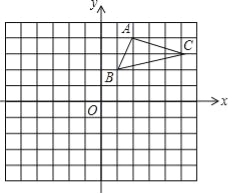
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.
查看答案和解析>>
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:解答题
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.
【答案】(1)作图见解析;点A1的坐标(2,﹣4);(2)作图见解析;点A2的坐标(﹣2,4).
【解析】
试题分析:(1)分别找出A、B、C三点关于x轴的对称点,再顺次连接,然后根据图形写出A点坐标;
(2)将△A1B1C1中的各点A1、B1、C1绕原点O旋转180°后,得到相应的对应点A2、B2、C2,连接各对应点即得△A2B2C2.
试题解析:(1)如图所示:点A1的坐标(2,﹣4);
(2)如图所示,点A2的坐标(﹣2,4).
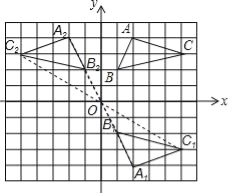
考点:1.作图-旋转变换;2.作图-轴对称变换.
【题型】解答题
【结束】
18
观察下面的点阵图和相应的等式,探究其中的规律:
(1)认真观察,并在④后面的横线上写出相应的等式.

①1=1 ②1+2=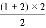 =3 ③1+2+3=
=3 ③1+2+3=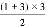 =6 ④ …
=6 ④ …
(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.

1=12②1+3=22③3+6=32④6+10=42⑤ …
(3)通过猜想,写出(2)中与第n个点阵相对应的等式 .
查看答案和解析>>
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:解答题
观察下面的点阵图和相应的等式,探究其中的规律:
(1)认真观察,并在④后面的横线上写出相应的等式.

①1=1 ②1+2=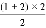 =3 ③1+2+3=
=3 ③1+2+3=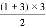 =6 ④ …
=6 ④ …
(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.

1=12②1+3=22③3+6=32④6+10=42⑤ …
(3)通过猜想,写出(2)中与第n个点阵相对应的等式 .
【答案】(1)10;(2)见解析;(3)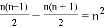
【解析】试题分析:(1)根据①②③观察会发现第四个式子的等号的左边是1+2+3+4,右边分子上是(1+4)×4,从而得到规律;
(2)通过观察发现左边是10+15,右边是25即5的平方;
(3)过对一些特殊式子进行整理、变形、观察、比较,归纳出一般规律.
试题解析:(1)根据题中所给出的规律可知:1+2+3+4=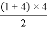 =10;
=10;
(2)由图示可知点的总数是5×5=25,所以10+15=52.
(3)由(1)(2)可知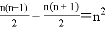
点睛:主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目中的难点.
【题型】解答题
【结束】
19
如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)
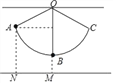
查看答案和解析>>
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:解答题
如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)
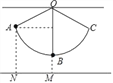
【答案】15cm
【解析】试题分析:设细线OB的长度为xcm,作AD⊥OB于D,证出四边形ANMD是矩形,得出AN=DM=14cm,求出OD=x-9,在Rt△AOD中,由三角函数得出方程,解方程即可.
试题解析:设细线OB的长度为xcm,作AD⊥OB于D,如图所示:
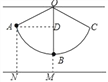
∴∠ADM=90°,
∵∠ANM=∠DMN=90°,
∴四边形ANMD是矩形,
∴AN=DM=14cm,
∴DB=14﹣5=9cm,
∴OD=x﹣9,
在Rt△AOD中,cos∠AOD=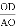 ,
,
∴cos66°=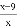 =0.40,
=0.40,
解得:x=15,
∴OB=15cm.
【题型】解答题
【结束】
20
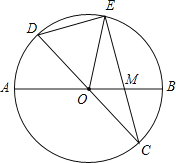
已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=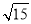 .
.
(1)求证:AM•MB=EM•MC;
(2)求EM的长;
(3)求sin∠EOB的值.
查看答案和解析>>
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:解答题
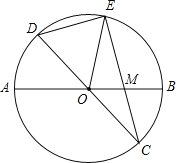
已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=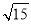 .
.
(1)求证:AM•MB=EM•MC;
(2)求EM的长;
(3)求sin∠EOB的值.
【答案】(1)证明见解析(2)4(3)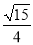
【解析】(1)连接A、C,E、B点,那么只需要求出△AMC和△EMB相似,即可求出结论,根据圆周角定理可推出它们的对应角相等,即可得△AMC∽△EMB;
(2)根据圆周角定理,结合勾股定理,可以推出EC的长度,根据已知条件推出AM、BM的长度,然后结合(1)的结论,很容易就可求出EM的长度;
(3)过点E作EF⊥AB,垂足为点F,通过作辅助线,解直角三角形,结合已知条件和(1)(2)所求的值,可推出Rt△EOF各边的长度,根据锐角三角函数的定义,便可求得sin∠EOB的值.
【题型】解答题
【结束】
21
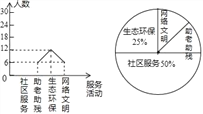
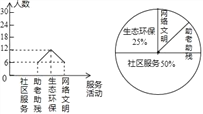
为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,合肥市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)请把折线统计图补充完整;
(2)求扇形统计图中,网络文明部分对应的圆心角的度数;
(3)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.
查看答案和解析>>
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:解答题
为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,合肥市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)请把折线统计图补充完整;
(2)求扇形统计图中,网络文明部分对应的圆心角的度数;
(3)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.
【答案】(1)见解析;(2)45°;(3)
【解析】试题分析:(1)根据参加生态环保的人数以及百分比求得总人数,用总人数乘以“社区服务”百分比求得其人数,即可解决问题;
(2)根据圆心角=360°×百分比,计算即可;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与他们参加同一服务活动的情况,再利用概率公式求解即可求得答案.
试题解析:(1)该班全部人数:12÷25%=48人.
社区服务的人数为48×50%=24,
补全折线统计如图所示:

(2)网络文明部分对应的圆心角的度数为360°× =45°;
=45°;
(3)分别用A,B,C,D表示“社区服务、助老助残、生态环保、网络文明”四个服务活动,
画树状图得:
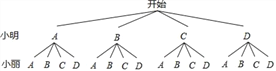
∵共有16种等可能的结果,他们参加同一服务活动的有4种情况,
∴他们参加同一服务活动的概率为 .
.
【题型】解答题
【结束】
22
某旅行社推出一条成本价位500元/人的省内旅游线路,游客人数y(人/月)与旅游报价x(元/人)之间的关系为y=﹣x+1300,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)求经营这条旅游线路每月所需要的最低成本;
(3)档这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
查看答案和解析>>
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:解答题
某旅行社推出一条成本价位500元/人的省内旅游线路,游客人数y(人/月)与旅游报价x(元/人)之间的关系为y=﹣x+1300,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)求经营这条旅游线路每月所需要的最低成本;
(3)档这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
【答案】(1)取值范围为1100元/人~1200元/人之间;(2)50000;(3)x=900时,w最大=160000
【解析】试题分析:(1)根据题意列不等式求解可;
(2)根据报价减去成本可得到函数的解析式,根据一次函数的图像求解即可;
(3)根据利润等于人次乘以价格即可得到函数的解析式,然后根据二次函数的最值求解即可.
试题解析:(1)∵由题意得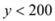 时,即
时,即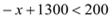 ,
,
∴解得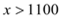
即要将该旅游线路每月游客人数控制在200人以内,该旅游线路报价的取值范围为1100元/人~1200元/人之间;
(2) ,
,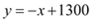 ,∴
,∴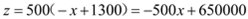
∵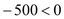 ,∴当
,∴当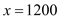 时,z最低,即
时,z最低,即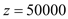 ;
;
(3)利润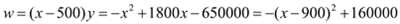
当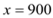 时,
时,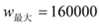 .
.
【题型】解答题
【结束】
23
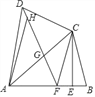
已知四边形ABCD中,AB=AD,对角线AC平分∠DAB,过点C作CE⊥AB于点E,点F为AB上一点,且EF=EB,连接DF.
(1)求证:CD=CF;
(2)连接DF,交AC于点G,求证:△DGC∽△ADC;
(3)若点H为线段DG上一点,连接AH,若∠ADC=2∠HAG,AD=3,DC=2,求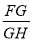 的值.
的值.
查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级第一次模拟考试数学试卷 题型:单选题
下面调查中,适合采用普查的是( )
A. 调查全国中学生心理健康现状 B. 调查你所在的班级同学的身高情况
C. 调查50枚导弹的杀伤半径 D. 调查扬州电视台《今日生活》收视率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com