
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:单选题
如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
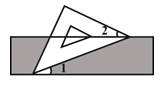
A. 15° B. 20° C. 25° D. 30°
查看答案和解析>>
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:单选题
下列关于x的一元二次方程有实数根的是( )
A. x2+1=0 B. x2+x+1=0 C. x2﹣x+1=0 D. x2﹣x﹣1=0
查看答案和解析>>
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:单选题
某企业因春节放假,二月份产值比一月份下降20%,春节后生产呈现良好上升势头,四月份比一月份增长15%,设三、四月份的月平均增长率为x,则下列方程正确的是( )
A. (1﹣20%)(1+x)2=1+15% B. (1+15%%)(1+x)2=1﹣20%
C. 2(1﹣20%)(1+x)=1+15% D. 2(1+15%)(1+x)=1﹣20%
查看答案和解析>>
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:单选题
某企业因春节放假,二月份产值比一月份下降20%,春节后生产呈现良好上升势头,四月份比一月份增长15%,设三、四月份的月平均增长率为x,则下列方程正确的是( )
A. (1﹣20%)(1+x)2=1+15% B. (1+15%%)(1+x)2=1﹣20%
C. 2(1﹣20%)(1+x)=1+15% D. 2(1+15%)(1+x)=1﹣20%
【答案】A
【解析】试题分析:根据题意可知二月份的产值为(1-20%),然后根据平均增长率为x可知四月份的产值是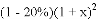 ,再根据四月比一月增长15%,可知
,再根据四月比一月增长15%,可知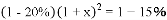 .
.
故选:A
【题型】单选题
【结束】
9
在同一平面坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A. 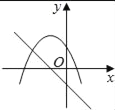 B.
B. 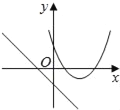 C.
C. 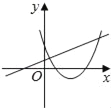 D.
D. 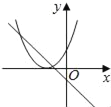
查看答案和解析>>
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:单选题
在同一平面坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A. 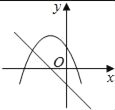 B.
B. 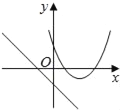 C.
C. 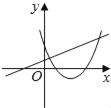 D.
D. 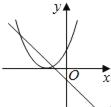
【答案】D
【解析】A.由函数y=mx+m的图象可知m<0,即函数y=?mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B.由函数y=mx+m的图象可知m<0,对称轴为x=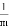 <0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C.由函数y=mx+m的图象可知m>0,即函数y=?mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D.由函数y=mx+m的图象可知m<0,即函数y=?mx2+2x+2开口方向朝上,对称轴为x=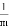 <0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
<0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
故选:D.
【题型】单选题
【结束】
10
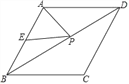
如图,已知菱形ABCD的周长为16,面积为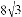 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
A. 2 B. 2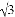 C. 4 D. 4
C. 4 D. 4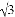
查看答案和解析>>
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:填空题
如图,已知菱形ABCD的周长为16,面积为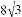 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
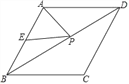
A. 2 B. 2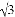 C. 4 D. 4
C. 4 D. 4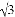
【答案】B
【解析】试题解析:如图作CE′⊥AB于E′,交BD于P′,连接AC、AP′.
∵已知菱形ABCD的周长为16,面积为8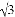 ,
,
∴AB=BC=4,AB•CE′=8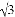 ,
,
∴CE′=2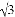 ,
,
在Rt△BCE′中,BE′=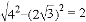 ,
,
∵BE=EA=2,
∴E与E′重合,
∵四边形ABCD是菱形,
∴BD垂直平分AC,
∴A、C关于BD对称,
∴当P与P′重合时,P′A+P′E的值最小,最小值为CE的长=2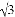 ,
,
故选:B.
【题型】单选题
【结束】
11
9的平方根是_____.
查看答案和解析>>
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:填空题
9的平方根是_____.
【答案】±3
【解析】试题解析:∵(±3)2=9,
∴±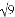 =±3
=±3
故9的平方根是±3.
故答案为:±3.
【题型】填空题
【结束】
12
分解因式:a3﹣2a2+a=________.
查看答案和解析>>
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:填空题
分解因式:a3﹣2a2+a=________.
【答案】a(a﹣1)2
【解析】试题分析:此多项式有公因式,应先提取公因式a,再对余下的多项式进行观察,有3项,可利用完全平方公式继续分解.a3﹣2a2+a=a(a2﹣2a+1)=a(a﹣1)2.故答案为:a(a﹣1)2.
考点:提公因式法与公式法的综合运用.
【题型】填空题
【结束】
13
如图,正五边形ABCDE的边长为2,分别以点C、D为圆心,CD长为半径画弧,两弧交于点F,则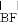 的长为_____.
的长为_____.
查看答案和解析>>
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:填空题
如图,正五边形ABCDE的边长为2,分别以点C、D为圆心,CD长为半径画弧,两弧交于点F,则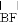 的长为_____.
的长为_____.
【答案】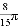
【解析】试题解析:连接CF,DF,
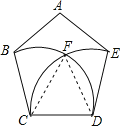
则△CFD是等边三角形,
∴∠FCD=60°,
∵在正五边形ABCDE中,∠BCD=108°,
∴∠BCF=48°,
∴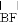 的长=
的长=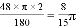 ,
,
故答案为: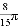 .
.
【题型】填空题
【结束】
14
矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
科目: 来源:安徽省合肥市庐阳区2018届九年级中考一模数学试卷 题型:解答题
矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
【答案】3或6
【解析】试题分析:
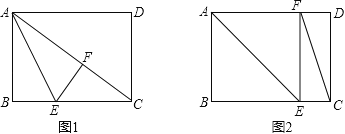
由题意可知有两种情况,见图1与图2;
图1:当点F在对角线AC上时,∠EFC=90°,
∵∠AFE=∠B=90°,∠EFC=90°,
∴点A、F、C共线,
∵矩形ABCD的边AD=8,
∴BC=AD=8,
在Rt△ABC中,AC=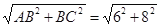 =10,
=10,
设BE=x,则CE=BC﹣BE=8﹣x,
由翻折的性质得,AF=AB=6,EF=BE=x,
∴CF=AC﹣AF=10﹣6=4,
在Rt△CEF中,EF2+CF2=CE2,
即x2+42=(8﹣x)2,
解得x=3,
即BE=3;
图2:当点F落在AD边上时,∠CEF=90°,
由翻折的性质得,∠AEB=∠AEF=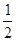 ×90°=45°,
×90°=45°,
∴四边形ABEF是正方形,
∴BE=AB=6,
综上所述,BE的长为3或6.
故答案为:3或6.
考点:1、轴对称(翻折变换);2、勾股定理
【题型】填空题
【结束】
15
计算:( )﹣2﹣
)﹣2﹣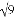 +(
+(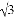 ﹣4)0﹣
﹣4)0﹣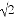 cos45°.
cos45°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com