
科目: 来源:广东省东莞市2018届九年级下学期第二次模拟考试数学试卷 题型:填空题
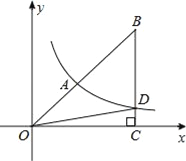
如图,双曲线y= 经过Rt△BOC斜边上的点A,且满足
经过Rt△BOC斜边上的点A,且满足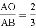 ,与BC交于点D,S△BOD=21,求k=__.
,与BC交于点D,S△BOD=21,求k=__.
查看答案和解析>>
科目: 来源:广东省东莞市2018届九年级下学期第二次模拟考试数学试卷 题型:解答题
已知等腰△ABC的顶角∠A=36°(如图).
(1)请用尺规作图法作底角∠ABC的平分线BD,交AC于点D(保留作图痕迹,不要求写作法);
(2)证明:△ABC∽△BDC.

查看答案和解析>>
科目: 来源:广东省东莞市2018届九年级下学期第二次模拟考试数学试卷 题型:解答题
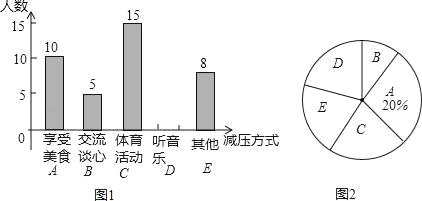
某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.
查看答案和解析>>
科目: 来源:广东省东莞市2018届九年级下学期第二次模拟考试数学试卷 题型:解答题
某商店第一次用300元购进笔记本若干,第二次又用300元购进该款笔记本,但这次每本的进价是第一次进价的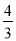 倍,购进数量比第一次少了25本.
倍,购进数量比第一次少了25本.
(1)求第一次每本笔记本的进价是多少元?
(2)若要求这两次购进的笔记本按同一价格全部销售完毕后获利不低于450元,问每本笔记本的售价至少是多少元?
查看答案和解析>>
科目: 来源:广东省东莞市2018届九年级下学期第二次模拟考试数学试卷 题型:解答题
如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)

查看答案和解析>>
科目: 来源:广东省东莞市2018届九年级下学期第二次模拟考试数学试卷 题型:解答题
如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)

【答案】8.7米
【解析】试题分析:首先利用三角形的外角的性质求得∠ACB的度数,得到BC的长度,然后在直角△BDC中,利用三角函数即可求解.
试题解析:∵∠CBD=∠A+∠ACB,
∴∠ACB=∠CBD﹣∠A=60°﹣30°=30°,
∴∠A=∠ACB,
∴BC=AB=10(米).
在直角△BCD中,CD=BCsin∠CBD=10× =5
=5 ≈5×1.732=8.7(米).
≈5×1.732=8.7(米).
答:这棵树CD的高度为8.7米.
考点:解直角三角形的应用
【题型】解答题
【结束】
23
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y= (m≠0)的图象相交于A(2,
(m≠0)的图象相交于A(2, ),B(-1,1)两点.
),B(-1,1)两点.
(1)分别求出反比例函数和一次函数的解析式;
(2)根据图象写出:当x为何值时,一次函数值大于反比例函数值?

查看答案和解析>>
科目: 来源:广东省东莞市2018届九年级下学期第二次模拟考试数学试卷 题型:解答题
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y= (m≠0)的图象相交于A(2,
(m≠0)的图象相交于A(2, ),B(-1,1)两点.
),B(-1,1)两点.
(1)分别求出反比例函数和一次函数的解析式;
(2)根据图象写出:当x为何值时,一次函数值大于反比例函数值?

【答案】(1)y= ,y=
,y= x-
x- ;(2)当x>2或-1<x<0时,一次函数值大于反比例函数值.
;(2)当x>2或-1<x<0时,一次函数值大于反比例函数值.
【解析】(1)根据题意,将A、B两点的坐标代入y=kx+b(k≠0)与y= ,即可得出解析式;
,即可得出解析式;
(2)求出一次函数图象在反比例函数图象的上方时,x的取值范围即可.
(1)∵反比例函数y= (m≠0)的图象经过点
(m≠0)的图象经过点 ,
,
∴ ,
,
∴m=1,
∴反比例函数的解析式为y= ,
,
∵一次函数y=kx+b(k≠0)的图象经过点A 和点B(-1,-1),
和点B(-1,-1),
∴ ,解得
,解得 ,
,
∴一次函数的解析式为y= x-
x- ;
;
(2)由图象,知当x>2或-1<x<0时,一次函数值大于反比例函数值.
【点睛】本题考查了一次函数和反比例函数的交点问题,熟练掌握待定系数法是解题的关键.
【题型】解答题
【结束】
24
如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4. 
(1)求证:  ~△ADB;
~△ADB;
(2) 求 的值;
的值;
(3)延长BC至F,连接FD,使 的面积等于
的面积等于 ,求证:DF与⊙O相切。
,求证:DF与⊙O相切。
查看答案和解析>>
科目: 来源:广东省东莞市2018届九年级下学期第二次模拟考试数学试卷 题型:解答题
如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4. 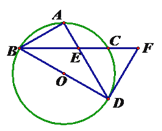
(1)求证: 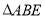 ~△ADB;
~△ADB;
(2) 求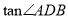 的值;
的值;
(3)延长BC至F,连接FD,使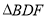 的面积等于
的面积等于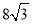 ,求证:DF与⊙O相切。
,求证:DF与⊙O相切。
【答案】(1)证明略
(2)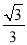
(3)60°
【解析】(1)
证明:∵点A是弧BC的中点,
∴∠ABC=∠ADB.
又∵∠BAE=∠DAB,
∴△ABE∽△ADB.…………………………………………………2分
(2)解
∵△ABE∽△ADB,
∴AB2=2×6=12.
∴AB=2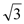 .
.
在Rt△ADB中,tan∠ADB=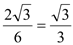 ………………………4分
………………………4分
(3)【解析】
连接CD,
∵tan∠ADB=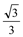 ,∴∠ADB=30°.
,∴∠ADB=30°.
又∵A为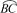 的中点,∴∠ABC=∠ADB=30°.
的中点,∴∠ABC=∠ADB=30°.
∵∠A=90°,∠ABD=60°.
∴∠DBC=30°.
∴CD=AB=2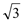 ,BE=DE=4.
,BE=DE=4.
又∵S△BDF=8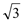 ,
,
∴BF=8.
∴EF=4.
又∵∠FED=∠EBD+∠EDB=60°,
∴△EFD为等边三角形.
∴∠EDF=60°…………………………………………………………7分
【题型】解答题
【结束】
25
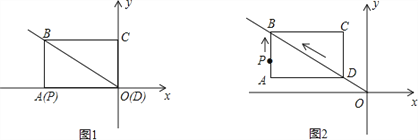
如图1,矩形ABCD的两条边在坐标轴上,点D与坐标原点O重合,且AD=8,AB=6.如图2,矩形ABCD沿OB方向以每秒1个单位长度的速度运动,同时点P从A点出发也以每秒1个单位长度的速度沿矩形ABCD的边AB经过点B向点C运动,当点P到达点C时,矩形ABCD和点P同时停止运动,设点P的运动时间为t秒.
(1)当t=5时,请直接写出点D、点P的坐标;
(2)当点P在线段AB或线段BC上运动时,求出△PBD的面积S关于t的函数关系式,并写出相应t的取值范围;
(3)点P在线段AB或线段BC上运动时,作PE⊥x轴,垂足为点E,当△PEO与△BCD相似时,求出相应的t值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com