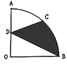
如图，在圆心角为90°的扇形OAB中，半径OA=4cm，C为弧AB的中点，D是OA的中点，则图中阴影部分的面积为________cm2．

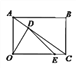
如图，在矩形ABCO中，AO=3， OC=4，设D、E分别是线段AC、OC上的动点，它们同时出发，点D以每秒3个单位的速度从点A向点C运动，点E以每秒1个单位的速度从点C向点O运动（不包含A、C两个端点）．当t=___________时，△ODE为直角三角形．

（1）计算：－2sin60°

（2）先化简，再求值：÷，其中

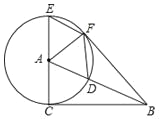
在Rt△ABC中，∠ACB=90°，以点A为圆心，AC为半径，作⊙A交AB于点D，交CA的延长线于点E，过点E作AB的平行线EF交⊙A于点F，连接AF、BF、DF

（1）求证：BF是⊙A的切线．

（2）当∠CAB等于多少度时，四边形ADFE为菱形？请给予证明．

2016年的母亲节，某校结合学生实际，计划开展了形式多样的感恩教育活动．下面图1，图2分别是该校调查部分学生是否知道母亲生日情况的扇形统计图和频数分布直方图．

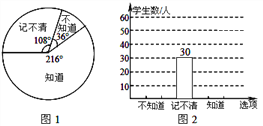
根据上图信息，解答下列问题：

（1）本次被调查的学生总人数有多少？

（2）补全频数分布直方图2；

（3）若这所学校共有学生3000人，已知被调查的学生中，知道母亲生日的女生人数是男生人数的2倍，请你通过计算估计该校知道母亲生日的女生有多少人？

已知关于x的一元二次方程（x－2）(x－3)＝m2，m为实数．

（1）求证：无论m为何值，方程总有两个不相等的实数根．

（2）m为何值时，方程有整数解．（直接写出三个，不需说明理由）

如图，禁渔期间，我渔政船在A处发现正北方向B处有一艘可疑船只，测得A、B两处距离为99海里，可疑船只正沿南偏东53°方向航行．我渔政船迅速沿北偏东27°方向前去拦截，2小时后刚好在C处将可疑船只拦截．求该可疑船只航行的速度．

（参考数据：sin27°≈， cos27°≈， tan27°≈， sin53°≈， cos53°≈， tan53°≈）

在某书店准备购进甲、乙两种图书共100本，购书款不高于2224元，两种图书的进价、售价如下表所示：

请解答下列问题：

(1)在这批图书全部售出的条件下，书店如何进货利润最大？最大利润是多少？

(2)书店计划用(1)中的最大利润购买单价分别为72元、96元的排球、篮球捐给贫困山区的学校，那么在钱恰好用尽的情况下，最多可以购买排球和篮球共多少个？

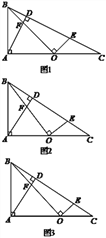
在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，点O是AC边上一点，连接BO，交AD于点F，OE⊥OB交BC于点E．

（1）如图1，当O为边AC中点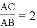，时，求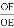的值.小明这样想的，过O点作OH∥AB交BC于点H，可证△AOF∽△HOE，于是求出答案，请你直接写出答案 ；

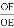（2）如图2，当O为边AC中点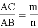，时，请求出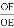的值,并说明理由；

（3）如图3，当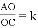,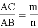时，请直接写出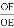的值．

如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，OC=OE=4，B为线段OA的中点，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M．

（1）求经过B、E、C三点的抛物线的解析式；

（2）若点P为线段FG上一个动点（与F、G不重合），当P在什么位置时，以P、O、C为顶点的三角形是等腰三角形，请求出此时点P的坐标；

（3）若点P为直线FG上一个动点，Q为抛物线上任一点，抛物线的顶点为N，探究以P、Q、M、N为顶点的四边形能否成为平行四边形？若能，请直接写出点P的坐标；若不能，请说明理由．