
科目: 来源:江西省等学校招生考试数学试卷 题型:解答题
如图,在四边形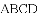
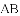
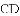
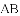
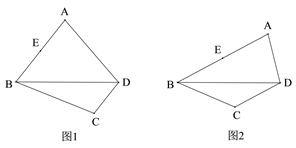
(1)在图1中,画出△ABD的BD边上的中线;
(2)在图2中,若BA=BD, 画出△ABD的AD边上的高 .
查看答案和解析>>
科目: 来源:江西省等学校招生考试数学试卷 题型:解答题
今年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.
抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)该班男生“小刚被抽中”是 事件,“小悦被抽中”是 事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为 ;
(2)试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠被抽中”的概率.
查看答案和解析>>
科目: 来源:江西省等学校招生考试数学试卷 题型:解答题
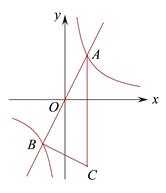
如图,反比例函数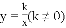 的图象与正比例函数
的图象与正比例函数 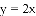
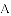
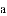
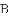
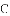
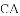
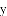
(1)求
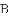
(2)求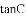
查看答案和解析>>
科目: 来源:江西省等学校招生考试数学试卷 题型:解答题
图1是一种折叠门,由上下轨道和两扇长宽相等的活页门组成,整个活页门的右轴固定在门框
上,通过推动左侧活页门开关;图2是其俯视图简化示意图,已知轨道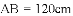
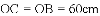
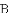
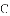
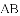
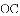
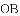
(1)若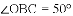
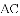
(2)当点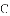
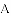
(参考数据:sin50°≈0.77, cos50°≈0.64, tan50°≈1.19, π取3.14)

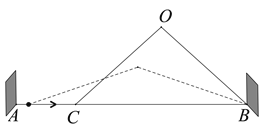
图1 图2
查看答案和解析>>
科目: 来源:江西省等学校招生考试数学试卷 题型:解答题
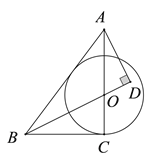
如图,在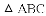
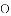
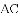
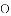
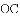
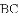
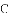
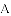
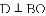
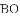
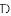

(1)求证: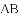
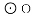
(2)若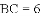
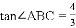 ,求
,求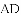
查看答案和解析>>
科目: 来源:江西省等学校招生考试数学试卷 题型:解答题
某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节,已知该蜜柚的成本价为8元/千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销售量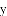
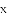
(1)求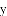
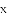
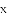
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
查看答案和解析>>
科目: 来源:江西省等学校招生考试数学试卷 题型:解答题
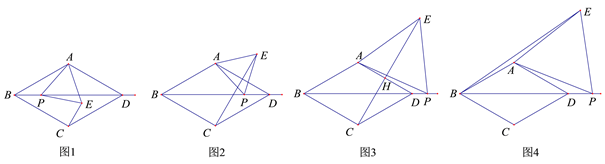
在菱形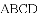
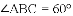
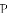
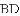
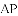
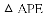
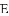
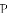
(1)如图1,当点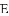
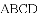
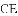

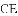
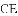
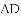
(2)当点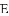
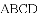
请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3) 如图4,当点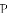
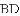
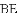
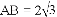 ,
,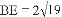 ,求四边形
,求四边形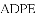
查看答案和解析>>
科目: 来源:江西省等学校招生考试数学试卷 题型:解答题
小贤与小杰在探究某类二次函数问题时,经历了如下过程:
求解体验
(1)已知抛物线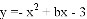 经过点(-1,0),则
经过点(-1,0),则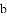
抽象感悟
我们定义:对于抛物线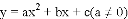 ,以
,以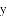
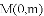
点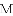
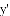
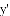
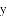
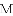
(2)已知抛物线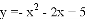 关于点
关于点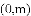
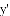
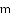
问题解决
(3) 已知抛物线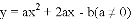
①若抛物线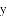
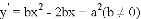 ,两抛物线有两个交点,且恰好是它们的顶点,求
,两抛物线有两个交点,且恰好是它们的顶点,求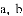
②若抛物线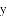
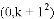 的衍生抛物线为
的衍生抛物线为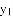 ,其顶点为
,其顶点为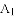 ;关于点
;关于点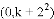 的衍生抛物线为
的衍生抛物线为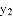 ,其顶点为
,其顶点为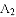 ;…;关于点
;…;关于点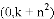 的衍生抛物线为
的衍生抛物线为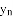 ,其顶点为
,其顶点为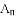 ;…(
;…(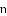
正整数).求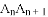 的长(用含
的长(用含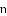

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com