
科目: 来源:重庆市巴南区七校共同体2017-2018学年八年级5月月考数学试卷 题型:填空题
高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲乙两车离B的距离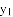 、
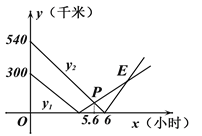
、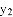 (千米)与行驶时间x(小时)之间的函数关系图象如图所示,交点P的横坐标为5.6,观察图象,给出下列结论:
(千米)与行驶时间x(小时)之间的函数关系图象如图所示,交点P的横坐标为5.6,观察图象,给出下列结论:
①A、C之间的路程为840千米;②乙车比甲车每小时快30千米;③当乙车到A点时,甲车距离B点250千米;④点E的坐标为(8,180).其中正确的有________________(填正确结论的序号).
查看答案和解析>>
科目: 来源:重庆市巴南区七校共同体2017-2018学年八年级5月月考数学试卷 题型:填空题
如图,已知△ABC中,AB=AC=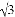 cm,∠BAC=120°,点P在BC上从C向B运动,点Q在AB、AC上沿B→A→C运动,点P、Q分别从点C、B同时出发,速度均为1cm/s,当其中一点到达终点时两点同时停止运动,则当运动时间t=_____s时,△PAQ为直角三角形.
cm,∠BAC=120°,点P在BC上从C向B运动,点Q在AB、AC上沿B→A→C运动,点P、Q分别从点C、B同时出发,速度均为1cm/s,当其中一点到达终点时两点同时停止运动,则当运动时间t=_____s时,△PAQ为直角三角形.

查看答案和解析>>
科目: 来源:重庆市巴南区七校共同体2017-2018学年八年级5月月考数学试卷 题型:填空题
如图,□ABCD中,∠A=60°,点E、F分别在边AD、DC上,DE=DF,且∠EBF=60°,若AE=2,FC=3,则EF的长度为_________________.

查看答案和解析>>
科目: 来源:重庆市巴南区七校共同体2017-2018学年八年级5月月考数学试卷 题型:解答题
已知某经济开发区有一块四边形空地ABCD,如图所示,现计划在该空地上种植草皮,经测量∠B=90°,AB=400m,AD=1300m,CD=1200m,BC=300m,请计算种植草皮的面积.

查看答案和解析>>
科目: 来源:重庆市巴南区七校共同体2017-2018学年八年级5月月考数学试卷 题型:解答题
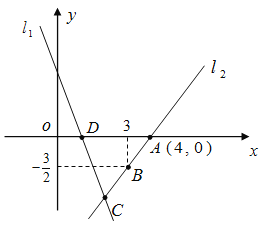
如图,直线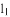 的解析表达式为
的解析表达式为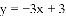
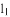 与
与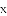
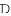
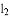 经过点
经过点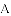
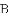
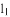 ,
,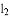 交于点
交于点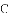
(1)求点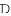
(2)求直线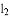 的解析表达式;
的解析表达式;
(3)求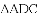
(4)在直线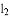 上存在异于点
上存在异于点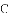
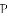
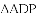
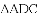
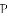
查看答案和解析>>
科目: 来源:重庆市巴南区七校共同体2017-2018学年八年级5月月考数学试卷 题型:解答题
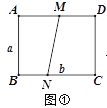
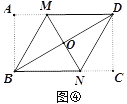
如图①,矩形纸片ABCD的边长分别为a、b(a<b),点M、N分别为边AD、BC上两点(点A、C除外),连接MN.
(1)如图②,分别沿ME、NF 将MN两侧纸片折叠,使点A、C分别落在MN上的A′、C′处,直接写出ME与FN的位置关系;
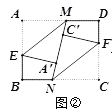
(2)如图③,当MN⊥BC 时,仍按(1)中的方式折叠,请求出四边形A′EBN与四边形C′FDM 的周长(用含a的代数式表示),并判断四边形A′EBN与四边形C′FDM周长之间的数量关系;
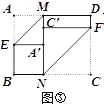
(3)如图④,若对角线BD与MN交于点O,分别沿BM、DN将MN两侧纸片折叠,折叠后,点A、C恰好都落在点O处,并且得到的四边形BNDM是菱形,请你探索a、b之间的数量关系.
查看答案和解析>>
科目: 来源:重庆市巴南区七校共同体2017-2018学年八年级5月月考数学试卷 题型:解答题
光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.
两地区与该农机租赁公司商定的每天的租赁价格见下表:

(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说明有多少种分派方案,并将各种方案设计出来;
(3)如何分派才能使这50台联合收割机每天获得的租金最高?
查看答案和解析>>
科目: 来源:重庆市巴南区七校共同体2017-2018学年八年级5月月考数学试卷 题型:解答题
在菱形ABCD中,∠BAD=60°
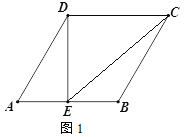
(1)如图1,点E为线段AB的中点,连接DE、CE,若AB=4,求线段EC的长;
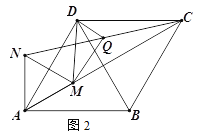
(2)如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论.
查看答案和解析>>
科目: 来源:重庆市巴南区七校共同体2017-2018学年八年级5月月考数学试卷 题型:解答题
已知直线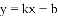

 )到直线
)到直线
 计算.
计算.
例如:求点P(-2,1)到直线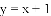
【解析】
因为直线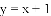
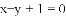


所以点P(-2,1)到直线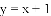
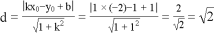 .
.
根据以上材料求:
(1)点P(2,-1)到直线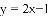
(2)已知M为直线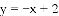
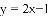
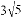 ,求M的坐标;
,求M的坐标;
(3)已知线段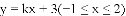
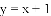
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com