
科目: 来源:人教版数学八年级上册 第12章《全等三角形》单元测试卷 题型:解答题
阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据.
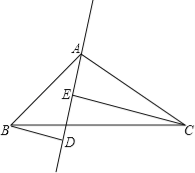
已知:如图,AM,BN,CP是△ABC的三条角平分线.
求证:AM、BN、CP交于一点.
证明:如图,设AM,BN交于点O,过点O分别作OD⊥BC,OF⊥AB,垂足分别为点D,E,F.
∵O是∠BAC角平分线AM上的一点( ),
∴OE=OF( ).
同理,OD=OF.
∴OD=OE( ).
∵CP是∠ACB的平分线( ),
∴O在CP上( ).
因此,AM,BN,CP交于一点.

查看答案和解析>>
科目: 来源:人教版数学八年级上册 第12章《全等三角形》单元测试卷 题型:解答题
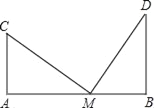
如图,两根旗杆AC与BD相距12m,某人从B点沿AB走向A,一定时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线夹角为90°,且CM=DM.已知旗杆AC的高为3m,该人的运动速度为0、5m/s,求这个人走了多长时间?
查看答案和解析>>
科目: 来源:人教版数学八年级上册 第12章《全等三角形》单元测试卷 题型:解答题
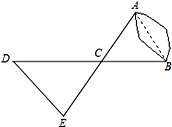
如图,A、B两点分别位于一个池塘的两侧,池塘西边有一座假山D,在DB的中点C处有一个雕塑,小川从点A出发,沿直线AC一直向前经过点C走到点E,并使CE=CA,然后他测量点E到假山D的距离,则DE的长度就是A、B两点之间的距离.
(1)你能说明小川这样做的根据吗?
(2)如果小川恰好未带测量工具,但是知道A和假山D、雕塑C分别相距200米、120米,你能帮助他确定AB的长度范围吗?
查看答案和解析>>
科目: 来源:人教版数学八年级上册 第12章《全等三角形》单元测试卷 题型:解答题
如图①,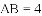
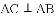
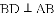
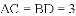
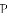
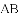
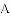
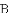
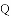
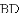
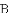
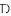

(1)若点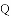
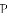
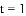
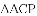
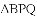
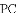
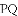
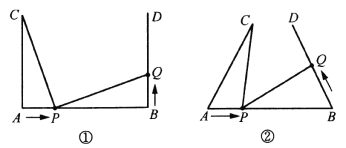
(2)如图②,将图①中的“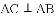
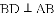
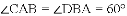
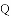
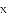
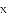
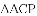
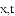
查看答案和解析>>
科目: 来源:人教版数学八年级上册 第12章《全等三角形》单元测试卷 题型:解答题
如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
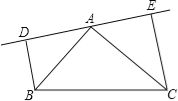
(2)若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
查看答案和解析>>
科目: 来源:2017-2018学年山东省济南市长清区八年级(下)期末数学试卷 题型:单选题
若一个多边形的内角和为外角和的3倍,则这个多边形为 ( )
A.八边形 | B.九边形 | C.十边形 | D.十二边形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com