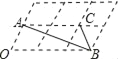
如图，6个形状、大小完全相同的菱形组成网格，菱形的顶点称为格点．已知菱形的一个角（∠O）为60°，A，B，C都在格点上，则tan∠ABC的值是_____．

在平行四边形ABCD中，BC边上的高为4，AB=5，AC=2，则平行四边形ABCD的周长等于_____．

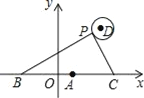
如图，在平面直角坐标系中，已知点A（1，0），B（1﹣a，0），C（1+a，0）（a＞0），点P在以D（4，4）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则a的最大值是_______．

如图，分别以直角△ABC的斜边AB，直角边AC为边向△ABC外作等边△ABD和等边△ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠ACB=90°，∠BAC=30°．给出如下结论：

①EF⊥AC；②四边形ADFE为菱形；③AD=4AG；④FH=BD

其中正确结论的为______（请将所有正确的序号都填上）．

（1）计算：|﹣|﹣+2sin60°+（）﹣1+（2﹣）0

（2）先化简，再求值： ÷（1﹣），其中a=﹣2．

如图，△ABC内接于⊙O，∠B=60°，CD是⊙O的直径，点P是CD延长线上的一点，且AP=AC．

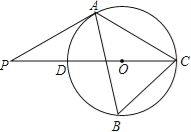
（1）求证：PA是⊙O的切线；

（2）若PD=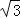，求⊙O的直径．

如图，正比例函数的图象与反比例函数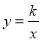的图象交于A、B两点，过点A作AC垂直x轴于点C，连结BC．若△ABC的面积为2．

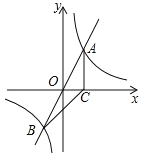
（1）求k的值；

（2）x轴上是否存在一点D，使△ABD为直角三角形？若存在，求出点D的坐标；若不存在，请说明理由．

在“母亲节”前夕，我市某校学生积极参与“关爱贫困母亲”的活动，他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖，要求每件销售价格不得高于27元，并将所得利润捐给贫困母亲。经试验发现，若每件按22元的价格销售时，每天能卖出42件；若每件按25元的价格销售时，每天能卖出33件．假定每天销售件数y（件）与销售价格x（元/件）满足一个以x为自变量的一次函数.

（1）求y与x满足的函数关系式（不要求写出x的取值范围）；

（2）在不积压且不考虑其他因素的情况下，销售价格定为多少元时，才能使每天获得的利润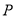最大，最大利润是多少？

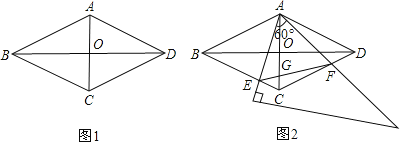
如图1，在菱形ABCD中，AC=2，BD=2 3 ，AC，BD相交于点O．

（1）求边AB的长；

（2）如图2，将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处，绕点A左右旋转，其中三角板60°角的两边分别与边BC，CD相交于点E，F，连接EF与AC相交于点G．

①判断△AEF是哪一种特殊三角形，并说明理由；

②旋转过程中，当点E为边BC的四等分点时（BE＞CE），求CG的长．

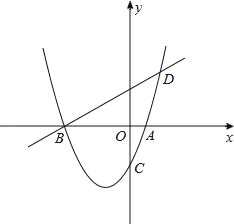
如图，已知抛物线y=ax2+bx﹣2（a≠0）与x轴交于A、B两点，与y轴交于C点，直线BD交抛物线于点D，并且D（2，3），tan∠DBA=．

（1）求抛物线的解析式；

（2）已知点M为抛物线上一动点，且在第三象限，顺次连接点B、M、C、A，求四边形BMCA面积的最大值；

（3）在（2）中四边形BMCA面积最大的条件下，过点M作直线平行于y轴，在这条直线上是否存在一个以Q点为圆心，OQ为半径且与直线AC相切的圆？若存在，求出圆心Q的坐标；若不存在，请说明理由．