
科目: 来源:2017-2018学年湖北省襄阳市宜城市九年级(上)期末数学试卷 题型:解答题
已知关于x的一元二次方程x2﹣4x+3m﹣2=0有两个不相等的实数根.
(1)求m的取值范围;
(2)当m为正整数时,求方程的根.
查看答案和解析>>
科目: 来源:2017-2018学年湖北省襄阳市宜城市九年级(上)期末数学试卷 题型:解答题
某市A,B两镇相距42千米,分别从A,B处测得某风景区中心C处的方位角如图所示,风景区区域是以C为圆心,15千米为半径的圆,tanα=1.673,tanβ=1.327.为了开发旅游,有关部门要设计修建连接A,B两市的县级公路.问连接A,B的两镇的县级公路是否穿过风景区,请说明理由.

查看答案和解析>>
科目: 来源:2017-2018学年湖北省襄阳市宜城市九年级(上)期末数学试卷 题型:解答题
列方程解应用题:
王师傅今年6月份开了一家商店,今年8月份开始盈利,9月份盈利2500元,11月份的盈利达到3600元,且从9月到11月,每月盈利的平均增长率都相同.
(1)求每月盈利的平均增长率;
(2)按照这个平均增长率,预计12月份这家商店的盈利能达到4300元吗?
查看答案和解析>>
科目: 来源:2017-2018学年湖北省襄阳市宜城市九年级(上)期末数学试卷 题型:解答题
盒中有x枚黑棋和y枚白棋,这些棋除颜色外无其他差别.
(1)从盒中随机取出一枚棋子,如果它是黑棋的概率是 ,写出表示x和y关系的表达式.
,写出表示x和y关系的表达式.
(2)往盒中再放进10枚黑棋,取得黑棋的概率变为 ,求x和y的值.
,求x和y的值.
查看答案和解析>>
科目: 来源:2017-2018学年湖北省襄阳市宜城市九年级(上)期末数学试卷 题型:解答题
如图,在平面直角坐标系xOy中,双曲线y= 经过?ABCD的顶点B,D.点D的坐标为(2,1),点A在y轴上,且AD∥x轴,S?ABCD=5.
经过?ABCD的顶点B,D.点D的坐标为(2,1),点A在y轴上,且AD∥x轴,S?ABCD=5.
(1)填空:点A的坐标为________;
(2)求双曲线和AB所在直线的解析式.

查看答案和解析>>
科目: 来源:2017-2018学年湖北省襄阳市宜城市九年级(上)期末数学试卷 题型:解答题
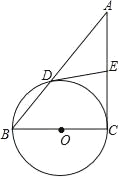
如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,DE交AC于点E,且∠A=∠ADE.
(1)求证:DE是⊙O的切线;
(2)若AD=16,DE=10,求BC的长.
查看答案和解析>>
科目: 来源:2017-2018学年湖北省襄阳市宜城市九年级(上)期末数学试卷 题型:解答题
某超市销售一种商品,成本每千克30元,规定每千克售价不低于成本,且不高于70元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 40 | 50 | 60 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入?成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目: 来源:2017-2018学年湖北省襄阳市宜城市九年级(上)期末数学试卷 题型:解答题
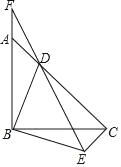
如图,在△ABC中,∠ABC=90°,AB=AC,点D在边AC上,将△ABD绕点B顺时针旋转得到△CBE,连接ED并延长交BA的延长线于点F.
(1)求证:∠CDE=∠ABD;
(2)探究线段AD,CD,BE之间的数量关系,并说明理由;
(3)若AD=1,CD=3,求线段EF的长.
查看答案和解析>>
科目: 来源:2017-2018学年湖北省襄阳市宜城市九年级(上)期末数学试卷 题型:解答题
如图,已知直线y=kx+6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,4)为抛物线的顶点,点B在x轴上.

(1)求抛物线的解析式;
(2)在(1)中抛物线的第三象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标.
查看答案和解析>>
科目: 来源:2018年秋人教版数学九年级上册同步练习:21.2.4根的判别式 题型:单选题
对于一元二次方程ax2+bx+c=0(a≠0),下列说法:
①b=a+c时,方程ax2+bx+c=0一定有实数根;
②若a、c异号,则方程ax2+bx+c=0一定有实数根;
③b2﹣5ac>0时方程ax2+bx+c=0一定有两个不相等的实数根;
④若方程ax2+bx+c=0有两个不相等的实数根,则方程cx2+bx+a=0也一定有两个不相等实数根.
其中正确的是( )
A. ①②③④ B. 只有①②③ C. 只有①②④ D. 只有②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com