
科目: 来源:人教版八年级上册 第十四章 整式的乘法与因式分解 单元测试卷 题型:解答题
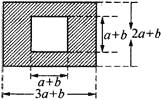
如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.
查看答案和解析>>
科目: 来源:人教版八年级上册 第十四章 整式的乘法与因式分解 单元测试卷 题型:解答题
某同学化简a(a+2b)﹣(a+b)(a﹣b)出现了错误,解答过程如下:
原式=a2+2ab﹣(a2﹣b2) (第一步)
=a2+2ab﹣a2﹣b2(第二步)
=2ab﹣b2 (第三步)
(1)该同学解答过程从第_____步开始出错,错误原因是____________;
(2)写出此题正确的解答过程.
查看答案和解析>>
科目: 来源:人教版八年级上册 第十四章 整式的乘法与因式分解 单元测试卷 题型:解答题
有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案:
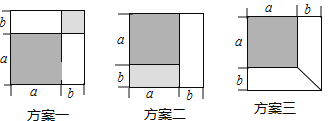
小明发现这三种方案都能验证公式:a2+2ab+b2=(a+b)2,对于方案一,小明是这样验证的:
a2+ab+ab+b2=a2+2ab+b2=(a+b)2
请你根据方案二、方案三,写出公式的验证过程.
方案二:
方案三:
查看答案和解析>>
科目: 来源:人教版八年级上册 第十四章 整式的乘法与因式分解 单元测试卷 题型:解答题
张老师在黑板上布置了一道题:
化简:2(x+1)2-(4x-5),并分别求出当x= 和x=-
和x=- 时代数式的值.
时代数式的值.
小亮和小新展开了下面的讨论,你认为他们两人谁说得对?并说明理由.

查看答案和解析>>
科目: 来源:人教版八年级上册 第十四章 整式的乘法与因式分解 单元测试卷 题型:解答题
(观察)1×49=49,2×48=96,3×47=141,…,23×27=621,24×26=624,25×25=625,26×24=624,27×23=621,…,47×3=141,48×2=96,49×1=49.
(发现)根据你的阅读回答问题:
(1)上述内容中,两数相乘,积的最大值为 ;
(2)设参与上述运算的第一个因数为a,第二个因数为b,用等式表示a与b的数量关系是 .
(类比)观察下列两数的积:1×59,2×58,3×57,4×56,…,m×n,…,56×4,57×3,58×2,59×1.
猜想mn的最大值为 ,并用你学过的知识加以证明.
查看答案和解析>>
科目: 来源:人教版八年级上册 第十四章 整式的乘法与因式分解 单元测试卷 题型:解答题
右侧练习本上书写的是一个正确的因式分解,但其中部分一次式被墨水污染看不清了.
(1)求被墨水污染的一次式;
(2)若被墨水污染的一次式的值不小于2,求x的取值范围.

查看答案和解析>>
科目: 来源:人教版八年级上册 第十四章 整式的乘法与因式分解 单元测试卷 题型:解答题
阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550﹣1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707﹣1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若ax=N(a>0,a≠1),那么x叫做以a为底N的对数,记作:x=logaN.比如指数式24=16可以转化为4=log216,对数式2=log525可以转化为52=25.
我们根据对数的定义可得到对数的一个性质:loga(M•N)=logaM+logaN(a>0,a≠1,M>0,N>0);理由如下:
设logaM=m,logaN=n,则M=am,N=an
∴M•N=am•an=am+n,由对数的定义得m+n=loga(M•N)
又∵m+n=logaM+logaN
∴loga(M•N)=logaM+logaN
解决以下问题:
(1)将指数43=64转化为对数式_____;
(2)证明loga =logaM﹣logaN(a>0,a≠1,M>0,N>0)
=logaM﹣logaN(a>0,a≠1,M>0,N>0)
(3)拓展运用:计算log32+log36﹣log34=_____.
查看答案和解析>>
科目: 来源:2018秋人教版七年级数学上册第四章几何图形初步 达标测试卷 题型:单选题
下列语句错误的是( )
A. 延长线段AB
B. 延长射线AB
C. 直线m和直线n相交于点P
D. 在射线AB上截取线段AC,使AC=3 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com