
科目: 来源:2018-2019学年度北师大版数学八年级上册 第1章《勾股定理》单元测试卷 题型:单选题
如图,圆锥的轴截面是边长为6cm的正三角形ABC,P是母线AC的中点,则在圆锥的侧面上从B点到P点的最短路线的长为( )
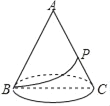
A. 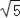 B. 2
B. 2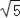 C. 3
C. 3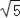 D. 4
D. 4
查看答案和解析>>
科目: 来源:2018-2019学年度北师大版数学八年级上册 第1章《勾股定理》单元测试卷 题型:填空题
如图是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,其中A、B、C、D的面积之和为16cm2,最大的正方形边长为_____cm.

查看答案和解析>>
科目: 来源:2018-2019学年度北师大版数学八年级上册 第1章《勾股定理》单元测试卷 题型:填空题
已知三角形ABC的三边长为a,b,c满足a+b=10,ab=18,c=8,则此三角形为______三角形.
查看答案和解析>>
科目: 来源:2018-2019学年度北师大版数学八年级上册 第1章《勾股定理》单元测试卷 题型:填空题
附加题:观察以下几组勾股数,并寻找规律:
①3,4,5;
②5,12,13;
③7,24,25;
④9,40,41;…
请你写出有以上规律的第⑤组勾股数:_____.
查看答案和解析>>
科目: 来源:2018-2019学年度北师大版数学八年级上册 第1章《勾股定理》单元测试卷 题型:填空题
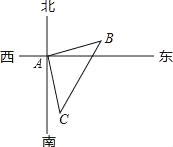
如图,在一次测绘活动中,某同学站在点A的位置观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为_____米(精确到0.1m).
查看答案和解析>>
科目: 来源:2018-2019学年度北师大版数学八年级上册 第1章《勾股定理》单元测试卷 题型:填空题
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,则小正方形的面积为_____(用a、b表示代数式)

查看答案和解析>>
科目: 来源:2018-2019学年度北师大版数学八年级上册 第1章《勾股定理》单元测试卷 题型:解答题
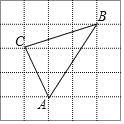
图中的小正方形边长为1,△ABC的三个顶点都在小正方形的顶点上,求
(1)△ABC的面积;
(2)边AC的长.
查看答案和解析>>
科目: 来源:2018-2019学年度北师大版数学八年级上册 第1章《勾股定理》单元测试卷 题型:解答题
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给
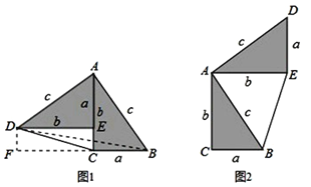
了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2 .
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a
∵S四边形ADCB=S△ACD+S△ABC= b2+
b2+ ab.
ab.
又∵S四边形ADCB=S△ADB+ S△DCB= c2+
c2+ a(b-a).
a(b-a).
∴ b2+
b2+ ab=
ab= c2+
c2+ a(b-a)
a(b-a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2.
查看答案和解析>>
科目: 来源:2018-2019学年度北师大版数学八年级上册 第1章《勾股定理》单元测试卷 题型:解答题
如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32.
(1)求∠BDC的度数;
(2)四边形ABCD的面积.

查看答案和解析>>
科目: 来源:2018-2019学年度北师大版数学八年级上册 第1章《勾股定理》单元测试卷 题型:解答题
三角形的周长为38,第一条边长为a,第二条边比第一条边的2倍多3.
(1)表示第三条边;
(2)若三角形为等腰三角形,求a的值;
(3)若a为正整数,此三角形是否为直角三角形?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com