Question

在△MNG中，已知NG=4，当动点M满足条件sinG-sinN=sinM时，求动点M的轨迹方程.

Answer 1

思路分析：本题主要考查双曲线的定义及标准方程的应用.根据双曲线的标准方程及题给条件，我们可以把已知关系进行转化，从而得到所要求的点的轨迹方程.

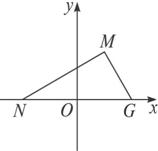
解：如图以NG所在的直线为x轴，以线段NG的垂直平分线为y轴建立直角坐标系.

∵sinG-sinN=sinM, ∴由正弦定理,得|MN|-|MG|=×4.

∴由双曲线的定义知，点M的轨迹是以N、G为焦点的双曲线的右支(除去与x轴的交点).

∴2c=4，2a=2，即c=2，a=1.∴b²=c²-a²=3.

∴动点M的轨迹方程为x²-=1(x＞0,且y≠0).

    方法归纳 求轨迹方程时，如果没有直角坐标系，应先建立适当的直角坐标系，动点M的轨迹是双曲线的一支并且去掉一个点.这种情况一般在求得方程的后面给以说明，并把说明的内容加上括号.