
(Ⅰ)当点P的横坐标为2时,求直线l的方程;
(Ⅱ)当点P在抛物线C上移动时,求线段PQ中点M的轨迹方程,并求点M到x轴的最短距离.
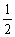
(21)本题主要考查直线、抛物线、不等式等基础知识,求轨迹方程的方法,解析几何的基本思想和综合解题能力.
解:(Ⅰ)把x=2代入y=![]() x2,得y=2,
x2,得y=2,
∴点P坐标为(2,2).
由y=![]() x2, ①
x2, ①
得y′=x,∴过点P的切线的斜率k切=2,直线l的斜率kl=-![]() =-
=-![]() ,
,
∴直线l的方程为y-2=-![]() (x-2),
(x-2),
即x+2y-6=0.
(Ⅱ)设P(x0,y0),则y0=![]() x02.
x02.
∵过点P的切线斜率k切=x0,当x0=0时不合题意,
∴x0≠0.∴直线l的斜率kl=-![]() =-
=-![]() ,
,
直线l的方程为y-![]() x02=-
x02=-![]() (x-x0). ②
(x-x0). ②
方法一:
联立①②消去y,得x2+![]() -2=0.
-2=0.
设Q(x1,y1),M(x,y).
∵M是PQ的中点,
∴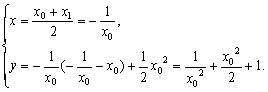
消去x0,得
y=x2+![]() +1(x≠0)就是所求的轨迹方程.
+1(x≠0)就是所求的轨迹方程.
由x≠0知x2>0,∴y=x2+![]() +1≥2
+1≥2![]() +1=
+1=![]() +1.
+1.
上式等号仅当x2=![]() ,即x=±
,即x=±![]() 时成立,所以点M到x轴的最短距离是
时成立,所以点M到x轴的最短距离是![]() +1.
+1.
方法二:
设Q(x1,y1),M(x,y),则
y0=![]() x02,y1=
x02,y1=![]() x12,x=
x12,x=![]() .
.
∴y0-y1=![]() x02-
x02-![]() x12=
x12=![]() (x0+x1)(x0-x1)=x(x0-x1),
(x0+x1)(x0-x1)=x(x0-x1),
∴x=![]() =kl=-
=kl=-![]() .
.
∴x0=-![]() .
.
将上式代入②并整理,得
y=x2+![]() +1(x≠0)就是所求的轨迹方程.
+1(x≠0)就是所求的轨迹方程.
由x≠0知x2>0,∴y=x2+![]() +1≥2
+1≥2![]() +1=
+1=![]() +1.
+1.
上式等号仅当x2=![]() ,即x=±
,即x=±![]() 时成立,所以点M到x轴的最短距离是
时成立,所以点M到x轴的最短距离是![]() +1.
+1.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
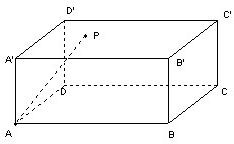 如图P是长方体AC′上底面内的一点,设AP与三个面A′C′、面A′B、面A′D所成的角为α,β,γ,则cos2α+cos2β+cos2γ=( )
如图P是长方体AC′上底面内的一点,设AP与三个面A′C′、面A′B、面A′D所成的角为α,β,γ,则cos2α+cos2β+cos2γ=( )| A、1 | ||
| B、2 | ||
C、
| ||
| D、随着P点的位置而定 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图P是△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC的中点,N是AB上的点,AN=3NB.其中Q是PB中点,S是AB的中点.求证:
如图P是△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC的中点,N是AB上的点,AN=3NB.其中Q是PB中点,S是AB的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:
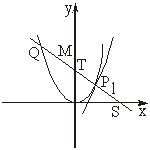
(Ⅰ)若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程;
(Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求![]() +
+![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com