
分析 由约束条件作出可行域,当x≥0,y≥0时,z=|x|+|y|=x+y,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解是坐标代入目标函数得z=|x|+|y|的最大值,由对称性可得z=|x|+|y|的最大值.
解答 解:由约束条件$\left\{\begin{array}{l}{|2x-y|≤2}\\{|2x+y|≤2}\end{array}\right.$作出可行域如图,
由图可知,当x≥0,y≥0时,z=|x|+|y|=x+y,过A时z有最大值为2,
则由对称性可知,z=|x|+|y|的最大值是2.
故答案为:2.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 26.5 | B. | 53 | C. | 31.5 | D. | 63 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
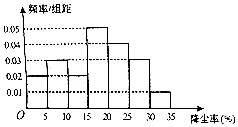 空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器---雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图:
空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器---雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (2,6)∪(6,10) | C. | (2,10) | D. | (2,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m=±2 | B. | m=2 | C. | m=-2 | D. | m≠±2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
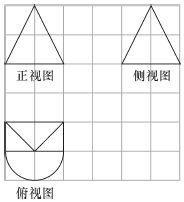 如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )
如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )| A. | $({1+\frac{{\sqrt{5}}}{2}})•π+2({1+\sqrt{5}})$ | B. | $\frac{{({1+\sqrt{5}})}}{2}•π+2({1+\sqrt{5}})$ | C. | $\frac{{({1+\sqrt{5}})}}{2}•π+2({3+\sqrt{5}})$ | D. | $\frac{{({1+\sqrt{5}})}}{2}•π+4+\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com