
分析 (1)利用二倍角的余弦公式求出cos2β的值;
(2)由sin(α-β)=$\frac{3}{5}$求出cos(α-β)的值,再由sinβ=$\frac{1}{3}$求出cosβ的值;利用sinα=sin[(α-β)+β]求出运算结果.
解答 解:(1)∵sinβ=$\frac{1}{3}$,
∴cos2β=1-2sin2β=1-2×${(\frac{1}{3})}^{2}$=$\frac{7}{9}$;
(2)∵α、β为锐角,
∴$α-β∈({-\frac{π}{2}\;,\;\;\frac{π}{2}})$;
又sin(α-β)=$\frac{3}{5}$,
∴cos(α-β)=$\sqrt{1{-(\frac{3}{5})}^{2}}$=$\frac{4}{5}$;
又sinβ=$\frac{1}{3}$,
∴cosβ=$\sqrt{1{-(\frac{1}{3})}^{2}}$=$\frac{2\sqrt{2}}{3}$;
∴sinα=sin[(α-β)+β]
=sin(α-β)cosβ+cos(α-β)sinβ
=$\frac{3}{5}$×$\frac{2\sqrt{2}}{3}$+$\frac{4}{5}$×$\frac{1}{3}$
=$\frac{6\sqrt{2}+4}{15}$.
点评 本题考查了三角恒等变换与同角的三角函数关系应用问题,是基础题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,单位位圆上的两个向量$\overrightarrow{a},\overrightarrow{b}$相互垂直,若向量$\overrightarrow{c}$满足($\overrightarrow{c}-\overrightarrow{a}$)•($\overrightarrow{c}-\overrightarrow{b}$)=0,则|$\overrightarrow{c}$|的取值范围是( )
如图所示,单位位圆上的两个向量$\overrightarrow{a},\overrightarrow{b}$相互垂直,若向量$\overrightarrow{c}$满足($\overrightarrow{c}-\overrightarrow{a}$)•($\overrightarrow{c}-\overrightarrow{b}$)=0,则|$\overrightarrow{c}$|的取值范围是( )| A. | [0,1] | B. | [0,$\sqrt{2}$] | C. | [1,$\sqrt{2}$] | D. | [1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{8\sqrt{3}}}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{{16\sqrt{3}}}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
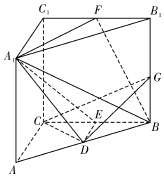 如图,三棱柱ABC-A1B1C1中,∠ACB=90°,CC1⊥底面ABC,AC=BC=CC1=2,D,E,F分别是棱AB,BC,B1C1的中点,G是棱BB1上的动点.
如图,三棱柱ABC-A1B1C1中,∠ACB=90°,CC1⊥底面ABC,AC=BC=CC1=2,D,E,F分别是棱AB,BC,B1C1的中点,G是棱BB1上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com