

| A. | $144+2\sqrt{10}π$ | B. | $144+({2\sqrt{10}-2})π$ | C. | $128+2\sqrt{10}π$ | D. | $128+({2\sqrt{10}-2})π$ |
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
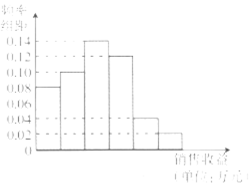 某公司为了解广告投入对销售收益的影响,在若干地区各投入万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从开始计数的.
某公司为了解广告投入对销售收益的影响,在若干地区各投入万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从开始计数的.| 广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
| 销售收益y(单位:万元) | 2 | 3 | 2 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<4} | B. | {x|x≤4} | C. | {x|1≤x<4} | D. | {x|1≤x≤4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 任何事件的概率总是在(0,1)之间 | |
| B. | 频率是客观存在的,与试验次数无关 | |
| C. | 概率是随机的,在试验前不能确定 | |
| D. | 随着试验次数的增加,频率一般会越来越接近概率 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,0] | B. | (-∞,-3]∪[0,+∞) | C. | [0,3] | D. | (-∞,0]∪[3,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com