考点:利用导数研究函数的单调性,函数在某点取得极值的条件
专题:导数的综合应用
分析:(1)当a=1时,f′(x)=
,由此利用导数性质能求出f(x)的极值.
(2)a>
时,f′(x)=
,由此利用分类讨论思想和导数性质能求出f(x)的单调区间.
解答:
解:(1)当a=1时,f′(x)=
| ex(x2+x+1)-ex(2x+1) |
| (x2+x+1)2 |
=
,
由f′(x)=0,得x=0或x=1,
当x∈(-∞,0)时,f′(x)>0;当x∈(0,1)时,f′(x)<0;
当x∈(1,+∞)时,f′(x)>0.
∴f(x)的增区间是(-∞,0),(1,+∞),减区间是(0,1),
∴f(x)
极小值=f(1)=
,f(x)
极大值=f(0)=1.
(2)a>
时,f′(x)=
| ex(x2+x+a)-ex(2x+1) |
| (x2+x+a)2 |
=
,
①当
<a<1时,由f′(x)>0,得x<
或x>
,
由f′(x)<0,得
<x<
,
∴f(x)的增区间是(-∞,
),(
,+∞),
减区间是(
,
);
②当a=1时,f(x)的增区间是(-∞,0),(1,+∞),减区间是(0,1);
③当1<a<
时,由f′(x)>0,得x<
或x>
,
由f′(x)<0,得
<x<
,
∴f(x)的增区间是(-∞,
),(
,+∞),
减区间是(
,
);
④当a≥
时,f′(x)>0,f(x)的增区间是(-∞,+∞).
点评:本题考查函数的极值的求法,考查函数的单调性的讨论,解题时要认真审题,注意导数性质和分类讨论思想的合理运用.



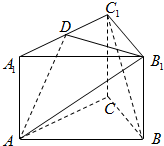 如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为
如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为