
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 由题意知本题是一个几何概型,概率等于对应面积之比,根据题意算出试验包含的总面积和符合条件的面积,求比值即可.
解答 解:设小方格边长为acm,
∵硬币的直径为2cm,显然a≥2;
使硬币与小方格的四边不相交,则
这时硬币所在的位置可以是以方格中心为中心点,以a-2为边长的方格;
且与小方格的四边不相交的概率不超过$\frac{1}{9}$,
即p=$\frac{{(a-2)}^{2}}{{a}^{2}}$≤$\frac{1}{9}$,
解出$\frac{3}{2}$≤a≤3,
即a的取值范围为[2,3]满足条件;
∴方格边长最长为3.
故选:A.
点评 本题考查了几何概型和面积的计算问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小值16 | B. | 最小值$\frac{1}{16}$ | C. | 最大值16 | D. | 最大值$\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 255 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
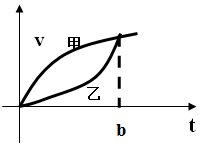 甲、乙速度v与时间t的关系如图,a(b)是t=b时的加速度,S(b)是从t=0到t=b的路程,则a甲(b)与a乙(b),S甲(b)与S乙(b)的大小关系是( )
甲、乙速度v与时间t的关系如图,a(b)是t=b时的加速度,S(b)是从t=0到t=b的路程,则a甲(b)与a乙(b),S甲(b)与S乙(b)的大小关系是( )| A. | a甲(b)>a乙(b),S甲(b)>S乙(b) | B. | a甲(b)<a乙(b),S甲(b)<S乙(b) | ||
| C. | a甲(b)<a乙(b),S甲(b)>S乙(b) | D. | a甲(b)<a乙(b),S甲(b)<S乙(b) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com