(实际应用题)在26枚崭新的金币中，混入了一枚外表与它们完全相同的假币(质量稍轻)，现在只有一台天平，请问：你最多称几次就可以发现这枚假币？

设f(x)是定义在[0，1]上的函数，若存在x^*∈(0，1)，使得f(x)在[0，x^*]上单调递增，在[x^*，1]上单调递减，则称f(x)为[0，1]上的单峰函数，x^*为峰点，包含峰点的区间为含峰区间．对任意的[0，1]上的单峰函数f(x)，下面研究缩短其含峰区间长度的方法：

(1)证明：对任意的x₁，x₂∈(0，1)，x₁＜x₂，若f(x₁)≥f(x₂)，则(0，x₂)为含峰区间；若f(x₁)≤f(x₂)，则(x₁，1)为含峰区间；

(2)对给定的r(0＜r＜0.5)，证明存在x₁，x₂∈(0，1)，满足x₂－x₁≥2r，使得由(1)所确定的含峰区间的长度不大于0.5＋r；

(3)选取x₁，x₂∈(0，1)，x₁＜x₂，由(1)可确定含峰区间为(0，x₂)或(x₁，1)，在所得的含峰区间内选取x₃，由x₃与x₁或x₃与x₂类似地可确定一个新的含峰区间．在第一次确定的含峰区间为(0，x₂)的情况下，试确定x₁，x₂，x₃的值，满足两两之差的绝对值不小于0.02，且使得新的含峰区间的长度缩短到0.34．

(区间长度等于区间的右端点与左端点之差)

若二次函数y＝－x²＋mx－1的图象与两端点为A(0，3)、B(3，0)的线段AB有两个不同的交点，求m的取值范围．

如图，有一块边长为15 cm的正方形铁皮，将其四个角各截去一个边长为x cm的小正方形，然后折成一个无盖的盒子．

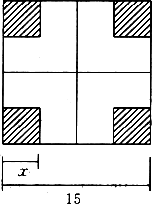
(1)求出盒子的体积y以x为自变量的函数解析式，并讨论这个函数的定义域；

(2)如果要做一个容积是150 cm³的无盖盒子，那么截去的小正方形的边长x是多少(精确到0.1 cm)？

求函数f(x)＝ln x＋2x－6的零点个数．

研究方程e^－x＝log₂x根的个数．

(创新应用题)已知函数y＝6x－2x²－m的值恒小于0，求m的取值范围．

分别在下列范围内求函数y＝x²－2x－3的最大值或最小值．

(1)0＜x＜2；

(2)2≤x≤3；

(3)0≤x≤3．

如图，二次函数y＝－mx²＋4m的顶点坐标为(0，2)，矩形ABCD的顶点B、C在x轴上，A、D在抛物线上，矩形ABCD在抛物线与x轴所围成的图形内．

(1)求二次函数解析式；

(2)设A(x，y)，试求矩形ABCD的周长P关于x的函数关系式，并求x的取值范围；

(3)是否存在这样的矩形ABCD，使它的周长为9？试证明你的结论．

关于x的方程ax²－2(a＋1)x＋a－1＝0，求a为何值时：

(1)方程有一根；

(2)方程有一正一负根；

(3)两根都大于1；

(4)一根大于1，一根小于1．