在周长为48的Rt△MPN中，∠MPN＝90°，tan∠PMN＝，求以M、N为焦点，且过点P的双曲线方程．

双曲线＝1的两个焦点为F₁、F₂，点P是双曲线上的点，若PF₁⊥PF₂，求点P到x轴的距离．

P是双曲线＝1上一点，F₁、F₂是双曲线的两个焦点，且|PF₁|＝17，求|PF₂|的值．

学校科技小组在计算机上模拟航天器变轨返回试验．设计方案如图所示：航天器运行(按顺时针方向)的轨迹方程为＋＝1，变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、M(0，)为顶点的抛物线的实线部分，降落点为D(8，0)．观测点A(4，0)、B(6，0)同时跟踪航天器．

(1)求航天器变轨后的运行轨迹所在的曲线方程；

(2)试问：当航天器在x轴上方时，观测点A、B测得离航天器距离分别为多少时，向航天器发出变轨指令？

小明家中有两种酒杯，一种酒杯的轴截面是等腰直角三角形，称之为直角酒杯(如图(1))，另一种酒杯的轴截面近似一条抛物线，杯口宽4 cm，杯深为8 cm(如图(2))，称之为抛物线酒杯．

(1)请选择适当的坐标系，求出抛物线酒杯的方程．

(2)一次，小明在游戏中注意到一个现象，若将一些大小不等的玻璃球依次放入直角酒杯中，则任何玻璃球能触及酒杯杯底．但若将这些玻璃球放入抛物线酒杯中，则有些小玻璃球能触及酒杯杯底．小明想用所学过的数学知识研究一下，当玻璃球的半径r为多大值时，玻璃球一定会触及酒杯杯底部．你能帮助小明解决这个问题吗？

过抛物线y²＝2px(p＞0)的焦点F，引两条相互垂直的弦AC、BD，求四边形ABCD面积的最小值．

在平面直角坐标系xOy中，抛物线y＝x²上异于坐标原点O的两不同动点A、B满足AO⊥BO(如图所示)．

(1)求△AOB的重心G(即三角形三条中线的交点)的轨迹方程；

(2)△AOB的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．

已知抛物线x²＝4y，点P是此抛物线上一动点，点A坐标为(12，6)，求点P到点A的距离与到x轴距离之和的最小值．

如图，已知抛物线的焦点为F(5，1)，准线方程为x＝1．

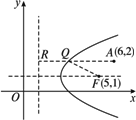
(1)求抛物线方程；

(2)求焦点到顶点的距离；

(3)求顶点坐标．

在已知抛物线y＝x²上存在两个不同的点M、N关于直线l：y＝－kx＋对称，求k的取值范围．