定义在R上的函数f(x)满足f(x＋2)=f(x)，且f(－x)=－f(x)，当xÎ (0，1)时，．

(1)求f(x)在[－1，1]上的解析式．

(2)证明f(x)在(0，1)上是减函数．

(3)当λ取何值时，方程f(x)=λ在[－1，1]上有解．

设函数，其中mÎ R，集合M={m|m＞1}．

(1)求证：当mÎ M时，f(x)对所有实数x都有意义；反之，如果f(x)对所有实数x都有意义，那么mÎ M．

(2)当mÎ M时，求函数f(x)的最小值．

(3)求证：对每一个mÎ M，函数f(x)的最小值都不小于1．

确定常数a，使方程：

有解，并求出它的解．

某工厂从1949的年产值100万元增加到40年后1989年的500万元，如果每年年增长率相同，则每年年产值增长率是多少?

已知函数，求函数f(x)的定义域，并讨论它的奇偶性和单调性．

已知函数，．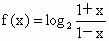

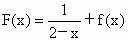(1)设F(x)的反函数为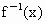，则方程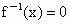有解吗?若有解，求出其解；若没有解，则说明理由．

(2)若f(x)的反函数为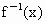，则对任意的自然数n(n>2)，是否都有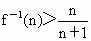成立?并说明理由．

已知函数，求函数的值域．

科学研究表明，宇宙射线在大气中能够产生放射性碳－14，碳－14的衰变极有规律，其精确性可以称为自然界的“标准时钟”．动植物在生长过程中衰变的碳－14，可以通过与大气的相互作用得到补充，所以活着的动植物每克组织中的碳－14含量保持不变．死亡后的动植物，停止了与外界环境的相互作用，机体中原有的碳－14按确定的规律衰减，我们已经知道其“半衰期”为5730年．

(1)设生物体死亡时，体内每克组织的碳－14含量为1，试推算生物死亡t年后体内每克组织中的碳－14含量P；

(2)湖南长沙马王堆汉墓女尸出土时碳－14的残余量约占原始含量的76.6％，试推算马王堆墓的年代．

已知函数f(x)=|x－a|，，且函数f(x)与g(x)的图象在y轴上的截距相等．

(1)求a的值；

(2)求函数f(x)＋g(x)的单调递增区间；

(3)若n为正整数，证明：．

(1)已知函数是单调递增的奇函数，定义域为[－1，1]，求函数的定义域和值域．

(2)证明：函数在区间[4，5]上是减函数．