
科目: 来源: 题型:044
(
北京海淀模拟)如下图,已知平行六面体 的底面为正方形,
的底面为正方形, 、O分别为上、下底面的中心,且
、O分别为上、下底面的中心,且 在底面ABCD上的射影是O.
在底面ABCD上的射影是O.

(1)
求证:平面 ⊥平面ABCD;
⊥平面ABCD;
(2)
若点E,F分别在棱 ,BC上,且
,BC上,且 ,问点F在何处时,EF⊥AD?
,问点F在何处时,EF⊥AD?
(3)
若 ,求二面角C-
,求二面角C- -B的大小(用反三角函数表示).
-B的大小(用反三角函数表示).查看答案和解析>>
科目: 来源: 题型:044
(2007
北京海淀模拟)如下图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°, ,E是BP的中点.
,E是BP的中点.
(1)
求证:EC∥平面APD;(2)
求BP与平面ABCD所成角的正切值;(3)
求二面角P-AB-D的大小.
查看答案和解析>>
科目: 来源: 题型:044
(2005
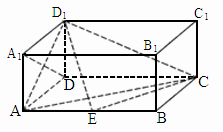
江西,20)如下图,在长方体 中,
中, ,AB=2,点E在棱AB上移动.
,AB=2,点E在棱AB上移动.
(1)
证明: ;
;
(2)
当E为AB的中点时,求点E到面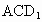 的距离;
的距离;
(3)AE
等于何值时,二面角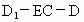 的大小为
的大小为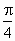 .
.查看答案和解析>>
科目: 来源: 题型:044
(2006
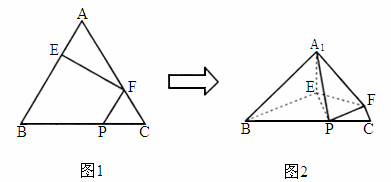
江苏,19)如下图,在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE∶EB=CF∶FA=CP∶PB=l∶2(如图1).将△AEF沿EF折起到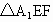 的位置,使二面角
的位置,使二面角 成直二面角,连结
成直二面角,连结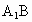 、
、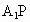 (如图2).
(如图2).
(1)
求证: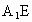 ⊥平面BEP;
⊥平面BEP;
(2)
求直线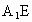 与平面
与平面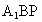 所成角的大小;
所成角的大小;
(3)
求二面角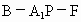 的大小(用反三角函数值表示).
的大小(用反三角函数值表示).查看答案和解析>>
科目: 来源: 题型:044
(2007
北京,16)如下图,在Rt△AOB中,∠OAB=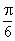 ,斜边AB=4,Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角.动点D在斜边AB上.
,斜边AB=4,Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角.动点D在斜边AB上.
(1)
求证:平面COD⊥平面AOB;(2)
当D为AB的中点时,求异面直线AO与CD所成角的大小;(3)
求CD与平面AOB所成角的最大值.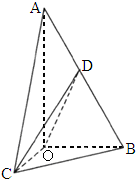
查看答案和解析>>
科目: 来源: 题型:044
(2007
北京海淀模拟)设关于x的方程 有两个实根α、β,且α<β.定义函数
有两个实根α、β,且α<β.定义函数 .
.
(1)
求αf(α)+βf(β)的值;(2)
判断f(x)在区间(α、β)上的单调性,并加以证明;(3)
若λ,μ为正实数,证明不等式: .
.查看答案和解析>>
科目: 来源: 题型:044
(2007
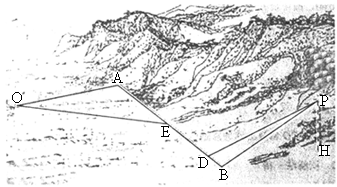
湖南,19)如图所示,某地为了开发旅游资源,欲修建一条连接风景点P和居民区O的公路.点P所在的山坡面与山脚所在水平面α所成的二面角为θ(0°<θ<90°),且 ,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用.从点O到山脚修路的造价为a万元/km,原有公路改建费用为
,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用.从点O到山脚修路的造价为a万元/km,原有公路改建费用为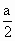 万元/km.当山坡上公路长度为lkm(1≤l≤2)时,其造价为
万元/km.当山坡上公路长度为lkm(1≤l≤2)时,其造价为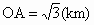 .
.
(1)
在AB上求一点D,使沿折线PDAO修建公路的总造价最小:(2)
对于(1)中得到的点D,在DA上求一点E,使沿折线PDEO修建公路的总造价最小;(3)
在AB上是否存在两个不同的点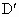 、
、 ,使沿折线
,使沿折线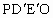 修建公路的总造价小于(2)中得到的最小总造价,证明你的结论.
修建公路的总造价小于(2)中得到的最小总造价,证明你的结论.查看答案和解析>>
科目: 来源: 题型:044
等腰直角三角形
AOB的直角边长为1.如图所示,在此三角形中任取点P,过P分别引三边的平行线,与各边围成以P为顶点的三个三角形(图中阴影部分),求这三个三角形的面积和的最小值,以及达到最小值时P的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com