(文)如图，已知长方体ABCD－A₁B₁C₁D₁中，AB＝BC＝1，BB₁＝2，连结BC₁，过点B₁作BC₁的垂线交CC₁于E．

(1)求证：AC₁⊥平面EB₁D₁；

(2)求三棱锥C₁－B₁D₁E的体积．

(理)在棱长为2的斜三棱柱ABC－DEF中，已知BF⊥AE，BF∩CE＝O，AB＝AE，连结AO．

(Ⅰ)求证：AO⊥平面FEBC；

(Ⅱ)求二面角B－AC－E的余弦值的大小；

(Ⅲ)求三棱锥B－DEF的体积．

(文)要将甲、乙两种大小不同的钢板截成A、B两种规格，每张钢板可同时截得A、B两种规格的小钢板的块数如下表所示：

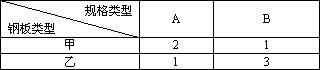
已知库房中现有甲、乙两种钢板的数量分别为5张和10张，市场急需A、B两种规格的成品数分别为15块和27块．

(1)问各截这两种钢板多少张可得到所需的成品数，且使所用的钢板张数最少？

(2)若某人对线性规划知识了解不多，而在可行域的整点中随意取出一解，求其恰好取到最优解的概率．

(理)甲有一只放有x个红球，y个黄球，z个白球的箱子，且x＋y＋a＝6(x，y，z∈N)，乙有一只放有3个红球，2个黄球，1个白球的箱子，两个各自从自己的箱子中任取一球，规定：当两球同色时甲胜，异色时乙胜．

(1)用x、y、z表示甲胜的概率；

(2)若又规定当甲取红、黄、白球而胜的得分分别为1、2、3分，否则得0分．求甲得分的期望的最大值及此时x、y、z的值．

△ABC中，a，b，c分别是角A，B，C的对边，且有．

(1)，求△ABC的面积；

(2)若，求的值．

长度为a(a＞0)的线段AB的两个端点A、B分别在x轴和y轴上滑动，点P在线段AB上，且(λ为常数且λ＞0)．

(Ⅰ)求点P的轨迹方程C；

(Ⅱ)当a＝λ＋1时，过点M(1，0)作两条互相垂直的直线l₁和l₂，l₁和l₂分别与曲线C相交于点N和Q(都异于点M)，试问：△MNQ能不能是等腰三角形？若能，这样的三角形有几个；若不能，请说明理由．

已知函数，其中x∈R，为参数，且．

(Ⅰ)当cos＝0时，判断函数f(x)是否有极值；

(Ⅱ)要使函数f(x)的极小值大于零，求参数的取值范围；

(Ⅲ)若对(Ⅱ)中所求的取值范围内的任意参数，函数f(x)在区间(2a－1，a)内都是增函数，求实数a的取值范围．

设数列{a_n}、{b_n}满足a_n＞0、b_n＞0且a_n＋b_n＝n(n∈N^*)．

①求M＝＋的最小值(用n表示)．

②设S_n＝a₁＋a₂＋……＋a_n，当M取得最小值时，求证：S_n＜2．

③设T_n＝b₁＋b₂＋……＋b_n，当M取得最小值时，求证：T_n＞．

(文)某种洗衣机洗涤衣服时，需经过进水、清洗、排水、脱水四个连续的过程．假设进水时水量匀速增加，清洗时水量保持不变．已知进水时间为4分钟，清洗时间为12分钟，排水时间为2分钟，脱水时间为2分钟．洗衣机中的水量y(升)与时间x(分钟)之间的关系如下表所示：

请根据表中提供的信息解答下列问题：

(1)试写出当x∈[0，16]时y关于x的函数解析式，并画出该函数的图象；

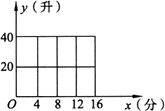
(2)根据排水阶段的2分钟点(x，y)的分布情况，可选用或y＝c(x－20)²＋d(其中a、b、c、d为常数)，作为在排水阶段的2分钟内水量y与时间x之间关系的模拟函数．试分别求出这两个函数的解析式．

已知函数

(Ⅰ)当a＞2时，求函数f(x)的极小值

(Ⅱ)试讨论曲线y＝f(x)与x轴的公共点的个数．