
科目: 来源:辽宁省实验中学2009届高三考前模拟数学试卷(理) 2009.6.1 题型:044
已知
C点在圆O直径BE的延长线上,CA切圆O于A点,∠ACB的平分线分别交AE、AB于点F、D.
(1)求∠ADF的度数;
(2)若AB=AC,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源:辽宁省实验中学2009届高三考前模拟数学试卷(理) 2009.6.1 题型:044
已知函数
f(x)=ax+lnx,x∈(1,e),且f(x)有极值.(1)求实数a的取值范围:
(2)求函数f(x)的值域;
(3)函数g(x)=x3-x-2,证明:![]() ,使得g(x0)=f(x1)成立.
,使得g(x0)=f(x1)成立.
查看答案和解析>>
科目: 来源:辽宁省实验中学2009届高三考前模拟数学试卷(理) 2009.6.1 题型:044
已知点
P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E: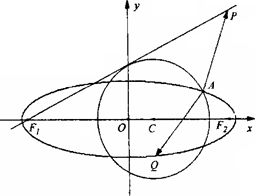
(Ⅰ)求m的值与椭圆E的方程;
(Ⅱ)设Q为椭圆E上的一个动点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:辽宁省实验中学2009届高三考前模拟数学试卷(理) 2009.6.1 题型:044
{an}是首项a1=4的等比数列,其前n项和为Sn,且S3,S2,S4成等差数列.
(1)求数列{an}的通项公式;
(2)若bn=log2|an|(n≥1,n∈N),设Tn为数列![]() 的前n项和,求证:
的前n项和,求证:![]() .
.
查看答案和解析>>
科目: 来源:辽宁省实验中学2009届高三考前模拟数学试卷(理) 2009.6.1 题型:044
如图,△
ABC与△ABP是边长为1的正三角形,O为AB的中点,且PO⊥面ABC,OE⊥PB,OF⊥PC.
(1)求三棱锥E-OCF的体积:
(2)设直线EF与平面ABC所成的角为![]() ,求cos
,求cos![]() 的值.
的值.
查看答案和解析>>
科目: 来源:辽宁省实验中学2009届高三考前模拟数学试卷(理) 2009.6.1 题型:044
2008年中国北京奥运会吉祥物由5个“中国福娃”组成,分别叫贝贝、晶晶、欢欢、迎迎、妮妮.现有8个相同的盒子,每个盒子中放一只福娃,每种福娃的数量如下表:
从中随机地选取
5只.(Ⅰ)求选取的5只恰好组成完整“奥运吉祥物”的概率;
(Ⅱ)若完整地选取奥运会吉祥物记10分;若选出的5只中仅差一种记8分;差两种记6分;以此类推.设ξ表示所得的分数,求ξ的分布列及数学期望.
查看答案和解析>>
科目: 来源:2009年高考数学文科(四川卷) 题型:044
设数列{an}的前n项和为sn,对任意的正整数n,都有an=5sn+1成立,记![]()
(Ⅰ)求数列{an}与数列{bn}的通项公式;
(Ⅱ)设数列{bn}的前n项和为Rn,是否存在正整数k,使得Rk≥4k成立?若存在,找出一个正整数k;若不存在,请说明理由;
(Ⅲ)记cn=b2n-b2n-1(n∈N+),设数列|cn|的前n项和味Tn,求证:对任意正整数n,都有![]()
查看答案和解析>>
科目: 来源:2009年高考数学文科(四川卷) 题型:044
已知椭圆![]() 的左、右焦点分别为F1、F2,离心率e=
的左、右焦点分别为F1、F2,离心率e=![]() ,右准线方程为x=2.
,右准线方程为x=2.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点F1的直线l与该椭圆相交于M、N两点,且![]() 求直线l的方程式.
求直线l的方程式.
查看答案和解析>>
科目: 来源:2009年高考数学文科(四川卷) 题型:044
已知函数f(x)=x3+2bx2+cx-2的图象在与x轴交点处的切线方程是y=5x-10.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设函数![]() 的极值存在,求实数m的取值范围以及函数g(x)取得极值时对应的自变量x的值.
的极值存在,求实数m的取值范围以及函数g(x)取得极值时对应的自变量x的值.
查看答案和解析>>
科目: 来源:2009年高考数学文科(四川卷) 题型:044
如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.

(Ⅰ)求证:EF⊥平面BCE;
(Ⅱ)设线段CD、AE的中点分别为P、M,求证:PM∥平面BCE;
(Ⅲ)求二面角F-BD-A的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com