设三角形abcd的对边长分别为a、b、c，且3b²＋3c²－3a²＝4bc．

(Ⅰ)求sinA的值：

(Ⅱ)求的值

在甲、乙等6个单位参加一次“唱读讲传”演出活动中，每个单位的节目安排在一起，若采用抽签的方式随机确定各单位的演出顺序(序号为1，2，…，6)，求

(Ⅰ)甲、乙两单位演出序号均为偶数的概率；

(Ⅱ)甲、乙两单位的演出序号不相邻的概率．

已知{a_n}是首项为19，公差为－2的等差数列，S_n 为{a_n}的前n项和．

(Ⅰ)求通项a_n及S_n

(Ⅱ)设{b_n－a_n}是首项为1，公比为3的等比数列，求数列{b_n}的通项公式及其前n项和T_n

设c₁，c₂…，c_n，…是坐标平面上的一列圆，它们的圆心都在x轴的正半轴上，且都与直线y＝x相切，对每一个正整数n，圆c_n都与圆c_n+1相互外切，以r_n表示c_n的半径，已知{r_n}为递增数列．

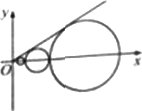
(Ⅰ)证明：{r_n}为等比数列；

(Ⅱ)设r¹＝1，求数列的前n项和．

设函数f(x)＝sinx－cosx＋x＋1，0＜x＜2∏，求函数f(x)的单调区间与极值．

如图，在多面体ABCDEF中，四边形ABCD是正方形，AB＝2EF＝2，EF∥AB，EF⊥FB，∠BFC＝90°，BF＝FC，H为BC的中点，

(Ⅰ)求证：FH∥平面EDB；

(Ⅱ)求证：AC⊥平面EDB；

(Ⅲ)求四面体B－DEF的体积．

某市20104月1日－4月30日对空气污染指数的检测数据如下(主要污染物为可吸入颗粒物)：

61，76，70，56，81，91，92，91，75，81，88，67，101，103，95，91，77，86，81，83，82，82，64，79，86，85，75，71，49，45，

(Ⅰ)完成频率分布表；

(Ⅱ)作出频率分布直方图；

(Ⅲ)根据国家标准，污染指数在0～50之间时，空气质量为优：在51～100之间时，为良；在101～150之间时，为轻微污染；在151～200之间时，为轻度污染．

请你依据所给数据和上述标准，对该市的空气质量给出一个简短评价．

椭圆E经过点A(2，3)，对称轴为坐标轴，焦点F₁，F₂在x轴上，离心率e＝．

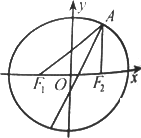
(1)求椭圆E的方程；

(2)求∠F₁AF₂的角平分线所在直线的方程．

△ABC的面积是30，内角A，B，C，所对边长分别为a，b，c，cosA＝．

(1)求；

(2)若c－b＝1，求a的值．

已知抛物线C：y²＝4x的焦点为F，过点K(－1，0)的直线l与C相交为A、B两点，点A关于x轴的对称点为D．

(Ⅰ)证明：点F在直线BD上；

(Ⅱ)设，求△BDK的内切圆M的方程．